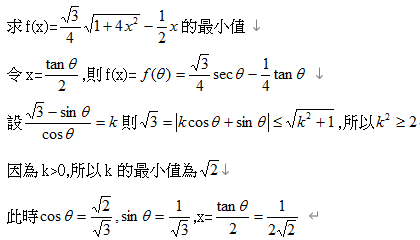高二進入空間座標系 根據研究 人類的空間概念通常較弱

從三垂線定理開始 一個定理要(1)會敘述 (2)證明 (3)應用 而三垂線定理的應用就是在求兩平面夾角

因此 以蜂巢為例 試試空間概念

是一個體積不變 表面積最小的問題 換句話說 是一個最節省材料的問題

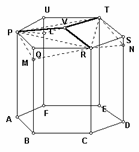蜂巢的一個蜂室就像這個樣子,外形是正六稜柱 (regular hexagonal prism)正六邊形PQRSTU是蜂室的正面，"屋頂"是三個全等的菱形(用蠟封住)，並與稜柱成等角。

左圖中,ABCDEF-PQRSTU是正六角柱，假設底面正六邊形PQRSTU的邊長=1 今截取MQ=NS=UL=x，並往上翻到V，使得PMRV，RNTV，PLTV是菱形。(則底面變成三個全等的菱形)

ABCDEF-PRT-V的體積與原來的六角柱不變，欲使ABCDEF-PRT-V的表面積有最小值，x=?

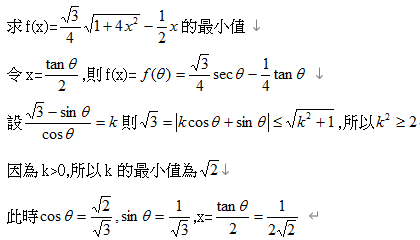
最小值的問題 高三的同學可以用微積分做

1. 希臘時代的Pappus就提出等周長問題(isoperimetric problem):
   在平面上，等周長的區域，以圓形面積最大。 他認為,蜜蜂把牠們的蜂巢作成正六邊形，顯示了某種程度的數學知能(mathematical understanding)。
   法國物理學家Monsieur de Reaumur認為，蜂巢的形狀是為了使材料最節省(容積固定，表面積最小)。因此向巴黎科學院院士Koenig請教。得到肯定的答案。
   材料最節省時,蜂室底部三個菱形，確實角 MPV=109度28分 與自然界實際的蜂巢相符。也就是說,蜜蜂確實以最省材料的方式建造牠們的蜂巢。
2. 甲烷CH4的結構HCH的夾角也是109度28分,不是巧合吧!據說一些礦石也有類似的結構(牛放屁 甲烷會讓地球升溫 所以要吃素 沒此一說)
3. 華羅庚科普著作選集 p.160
4. 100 Great Problems of Elementary Mathematics p.366 第93題 
5. 數學發現的趣談 蔡聰明
6. 數學歷史典故 梁宗巨 p.425
7. 蜂窩猜想 1999年由Thomas C. Hales解決了
8. 蜂巢結構的應用  紐約地標The Vessel
9. 蜜蜂與數學 Karl von Frisch 1886~1982