字體:小 中 大
字體:小 中 大 |
|
|
|
| 2021/04/01 11:39:46瀏覽274|回應0|推薦0 | |
其中 孟氏定理與塞瓦定理在20年前出現在高中數學課程綱要 有一本將近20頁的課本 討論共線性與共點性 非常困難 最後不了了之 孟氏定理 (Menelaus of Alexandria 約西元100年)
此處略去 ... ... 塞瓦定理(G.Ceva 1647~1734)
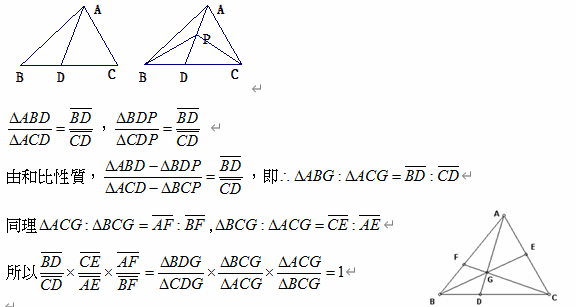
三角形的一個頂點與其對邊上任一點的連線稱為塞瓦線。 張景中(1936~),數學家,計算機科學家,中國科學院院士。多年從事幾何算法和定理機器證明研究,其成果曾獲國家發明二等獎,中國科學院自然科學一等獎,國家自然科學二等獎。 張先生有一個密技是面積法 塞瓦定理的證明用面積法是最明快的
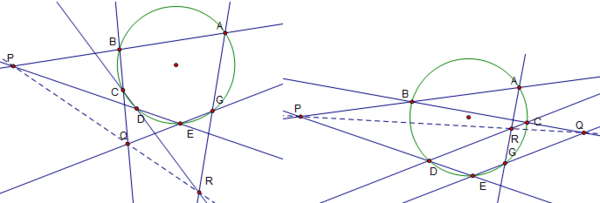
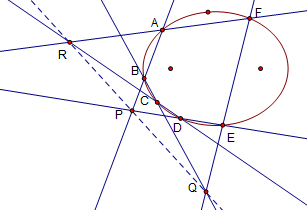
這裡 巴斯卡定理是其中一個有趣的定理 巴斯卡(B.Pascal 1623~1662)在16歲時發現的 圓內接六邊形ABCDEG(記為123456,(12,45)表示AB,DE交於P點,(23,56)表示Q點,(34,61)表示R點)則P,Q ,R共線(稱為巴斯卡線) 右圖是把C點拉到AG之間 也是一樣/...
把圓改成圓錐曲線(上圖是一橢圓) 巴斯卡定理仍然成立 這件事巴斯卡是知道的 這本書有很多有趣的東西 把這些東西應用到動態幾何 我想 清大全任重先生絕對是高手 可惜現在網頁為了安全 封鎖了動態的應用軟體 GSP無緣在網路上看到 [平面幾何中的幾個著名定理] |
|
| ( 創作|另類創作 ) |



 對於古典平面幾何有興趣的人 [
對於古典平面幾何有興趣的人 [
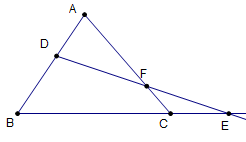 孟氏定理是用相似形證明的
孟氏定理是用相似形證明的