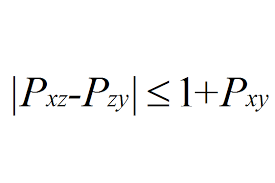
狗吉拉喜愛數學物理 
雖然讀附中實驗班時 物理數學都在20分30分徘徊

前兩天的諾貝爾物理獎 頒給了證"否"貝爾不等式(Bell inequality)的三位科學家
可是Bell大哥提出這個不等式是50多年前的事 
當時隨即就有一堆人運用各種實驗來"證實或證否"這個不等式到底成不成立
結果1960年代的不等式 到了2022年才被諾貝爾獎看上 
還真是一路艱辛啊 哈哈哈 以下分享狗吉拉在各種文獻裡看到的最淺顯(我最容易懂)的一篇
記錄在這裡當資料保存  
對物理有興趣的非專業物理學人 可以參考

https://www.getit01.com/p20180115227037773/
大家可以參考鏈結 去看原文 給作者(狗吉拉不知道他是誰)一個讚
狗吉拉盡量保留了原文 僅僅做了一些順順字眼的修改
===========================


貝爾不等式究竟是在闡述什麼問題？

在很多關於量子力學的書籍中，都不可避免的講到「貝爾不等式與量子糾纏」，
但坦白說，就我看到的書籍中，包括網上的資料，對此都「語焉不詳」或者「語焉太詳」，
所謂「語焉太詳」是說基本都如出一轍的上來就甩出一大堆公式，同時卻又對於這個不等式背後的邏輯究竟是什麼，
包括其究竟是在說什麼，最後的結論是什麼這些最基本的東西「語焉不詳」，
基本都是說，隨後阿斯派克特的實驗結果「突破了貝爾不等式所規定的限制」，從而證明了什麼什麼，
但是對於「貝爾不等式的限制」究竟是不允許什麼，卻又常常隻字不提，
直接就Jump到說是否定了愛因斯坦的理論，
但究竟否定的是什麼呢？
有的書裡說是否定了愛因斯坦的定域隱變數理論（據說愛因斯坦本人根本就不同意什麼隱變數理論）
有的書裡乾脆就還說是否定了物質的客觀存在性，
總之也可能是我讀書讀的太少吧，相關資料看了一大坨，也沒看到有一個真正很有條理的把整件事情給講清楚來龍去脈與其背後邏輯的，對此我也是醉了.....

好吧，丟掉這些吐槽不論，很想搞清楚以下幾個問題：
1）貝爾不等式究竟是在闡述一個什麼問題？其論證的邏輯是怎樣的？最終的結論又是什麼？
2）根據貝爾不等式，什麼事情是「理應受其限制」而不可能發生的呢？
3）阿斯派克特(Aspect)的實驗究竟在邏輯上是怎麼證明貝爾不等式是不成立的？
4）Aspect的實驗究竟是說明了什麼又否定了什麼？

我理解，所謂「量子糾纏」應該不是說如果宇宙的一端我們發現盒子里的是右手套，那麼立刻就能知道遠在另一端的盒子里一定是左手套那麼簡單淺顯無厘頭吧？

是的，這就是正解，任何過度的詮釋都是錯的。
就是我們發現這邊是左手套，根據某個奇怪的守恆律（例如一雙手套必然是一個左手套一個右手套），我們就可以斷言遠在宇宙另一端的另一個手套必然是右手套。

當然這不是古怪的地方，古怪的地方在於量子物理的不確定原理，
換言之在測量之前，你根本就不知道這是左手套還是右手套，
而測量之後，你不僅知道這個手套是左手套還是右手套，連著另一個手套你也知道是左還是右了。
這個"不知道"，更嚴格的說是"不確定"，也就是說不僅僅是你不知道，而是沒有任何人會知道，在你測量之前，這個手套就是左手套和右手套的疊加。

這當然是不符合直覺的，所以就有了隱變數詮釋，隱變數詮釋不僅僅可以解釋這個現象，還很符合我們的直覺。

手套不可能處於疊加態，事實上是因為我們不知道的另一個因素影響了手套到底是左手套還是右手套，處於糾纏態的兩個粒子這個因素是相反的，換言之一切都是確定的，而只是我們不知道而已。

這個解釋簡直太完美了，量子糾纏和不確定原理都可以被完美的解釋，而且非常符合我們的直覺。

鋪墊了這麼多，可以回答第一個問題了：


貝爾不等式究竟是在闡述一個什麼問題？

到底是不是存在這麼一個我們無法觀測的隱變數影響了我們的觀測結果，而不是因為量子真隨機現象。
其論證的邏輯是怎樣的？

貝爾證明了，如果真的存在一個隱變數，那麼多次測量的結果的分布概率，必然滿足貝爾不等式。
最終的結論又是什麼？

貝爾本身沒有給出結論，只是給出了驗證隱變數假設的方案。


補充的分隔線============================

我就知道科普文章老拿薛定諤的貓和EPR佯謬來舉例子遲早要出事兒的。正好借這個題目梳理一下。

怎樣解釋「薛定諤的貓」，能讓一個沒有高中數學基礎的人理解？

就像我在這個問題中的回答指出的一樣，很多人根本沒有指出一個重要的問題就是薛定諤的貓這個思想實驗本來就是用來抨擊量子力學的。

不確定性作為基本粒子的內稟屬性，根本就不是正常人能理解的事情，因為我們的現實世界顯然是確定的。怎麼去理解組成這個世界的基本組件是不確定的？

何況，在早期這根本就是個唯像的理論，也就是說我們通過觀察，或者通過論證，以我們所了解的觀測方式不可能同時確定位置和動量。
薛定諤的貓，和引發量子糾纏現象研究的EPR佯謬，都是兩個抨擊不確定性的思想實驗。

所以如果覺得量子物理毀三觀，無法接受不確定原理，一點兒也不要懷疑自己的智商，因為大牛如薛定諤，愛因斯坦一開始都是無法接受的！

薛定諤的貓本質上就是說，如果微觀世界是不確定的，那麼可以通過一個裝置我們可以把這個不確定性放大到宏觀世界，譬如有一隻貓這麼大。那麼根據哥本哈根詮釋，這貓是死和活的疊加態，這顯然是荒謬的，否則你給我找只又死又活的貓來？


而EPR佯謬則是說，如果不確定性確實是內稟屬性，那麼怎麼解釋兩個相隔極遠的粒子，在測量的時候不會違背守恆律呢？
這個佯謬的確沒有簡單的描述形式，我儘可能簡化一下就是這樣的：

假設有兩個粒子現在是抱在一起，沒有動能的（也就是說是靜止的），砰的一下，這倆粒子都獲得了動能，根據某個奇怪的守恆律，這倆粒子應該方向相反，速度一樣。但是不確定性說這兩個粒子的速度是不確定的，只有"實際去測量"才能得到確定的速度，
這時候問題來了，我隨便測量其中一個粒子，那另一個粒子的速度不就也知道了嗎？(否則守恆律就要被破壞了)。

EPR佯謬是對量子物理最致命的一擊，他指出，以下三個假設中只有可能有兩個是對的：守恆律、不確定性、局域性（不存在超距影響）。

結果TMD發現前兩個是對的，最後一個錯了，
毀三觀啊毀三觀。其實要我選，我寧可選擇守恆律是錯的啊，
XD。反正我是看熱鬧的不嫌事兒大。

當然物理學家都希望不確定性是錯的，誰給我把槍，我去斃了薛定諤的那隻貓，，，，

最後，在三個假設中，如果否定局域性，就是量子糾纏。否定不確定性，就是隱變數。否定守恆律，沒有物理學家敢這麼干啊，其實否定守恆律更好玩，為啥沒人以這個寫科幻呢？
貝爾不等式的意義在於，有了一個可以在實驗上驗證的方式，來證明局域實在理論和量子力學哪個是對的。

貝爾不等式有很多變種，下面以CHSH不等式為例來介紹貝爾不等式。
假設有兩個盒子A和B，各包含一個待測物理量。


如果給A提供輸入1，那麼它就以方式a測量這個物理量；如果給A提供輸入0，它就以方式b來測量這個物理量。得到的結果有兩種，記為x=0 or 1。

如果給B提供輸入1，那麼它就以方式c測量這個物理量；如果給B提供輸入0，它就以方式d來測量這個物理量。得到的結果有兩種，記為y=0 or 1。
如果可以滿足兩點要求
一，A和B的輸入是真隨機數，也就是所謂"free will"；（前陣子的大貝爾實驗的那個遊戲，大家不是要不停按0和1嘛~就是希望用大家的自由意志來提供真隨機數）
二，A和B之間的距離要足夠遠，使得A和B之間來不及通信。也就是說A和B的測量都不受對方的影響。
那麼局域實在論可以得到如下的不等式


而量子力學則可以得到S&>2的結果

其中 (X, Y)a, b
代表盒子A 輸入a，盒子B輸入b的時候，他們的結果的乘積的期望值。
所以只要實驗測出來S的值就可以知道哪個理論是對的了。

當然已經有很多實驗驗證站在了量子力學這一邊，只是這些實驗都有「漏洞」，主要有下面三個。

第一個漏洞就是隨機數漏洞。即使是量子隨機數，也是可能受隱變數控制的，
在這種情況下，局域實在論也可以得到S&>2的結果。
所以如果實驗中用的隨機數不是真隨機數，那麼即使得到S&>2的結果，也不能真的驗證局域實在論錯了。

第二個漏洞是局域漏洞。如果A和B之間距離不夠遠，也就是說在一方測量結束前，另一方的信息可以以不高於光速的速度傳遞過來的話，那麼即使在局域實在論下，也是可以得到S&>2的結果的。
所以只要實驗裡頭沒有滿足局域條件，即使得到S&>2的結果，也不能真的驗證局域實在論錯了。

第三個漏洞是測量漏洞。光傳輸過程中的損耗和探測器的不完美會降低整個系統的效率，也就是說不是所有的事件都能被測量到。如果系統總效率小於一定閾值的話，就無法排除結果被隱變數操控的可能，也就是說隱變數選擇了一些事件，使得這些事件可以得到S&>2的結果。
所以如果測量漏洞不關閉，即使得到S&>2的結果，也不能驗證局域實在論錯了。

不過去年已經有實驗同時關閉了局域漏洞和測量漏洞。
定域性和隱變數不相容。關於這一點，櫻井上有非常清晰的討論。
費曼這篇文章超級易讀，我從物理學逃離了5年之後發現這文章簡直比toefl閱讀還簡單


簡單來說，我們考慮一個A -&> B -&> C，在經典情況中

P(A,C) = int P(A,B) P(B,C) dB
然後量子力學下卻是
phi(A,C) = int phi(A,B) phi(B,C) dB
考慮到
P = phi^2
於是，物理學家表示前兩個方程，經典統計和波函數表示是不一致的，然後對統計學家發出了「你看看你」這種善意的笑聲
然後這群統計學家陷入憂鬱之中，甚至被一群寫代碼的搶了一部分機器學習/統計學習的工作。於是這群統計學家正在準確對這群寫代碼的人發出類似的善意的笑聲。
為什麼這兩個方程不一致呢，因為中間沒有對B觀測，於是缺一個確定的中間變數。


所以兩個方程背後的情境是不一樣的，經典統計B已經被觀測確定了，量子波函數下的B 卻沒有被確定

這又被稱為觀察喵效應~

好了，一個確定的 implicit variable可以看作一個確定的中間變數
我從邏輯上說一下理解吧，具體貝爾不等式的推導等專業的來補充。

貝爾證明了，如果有一個隱變數定理是正確的，那麼某物理量(兩個分隔的粒子同時被測量時其結果的可能關聯程度)一定會滿足一個限制(constraint)，
用數學表達出來就是貝爾不等式。

反過來，如果貝爾不等式給出的這個限制不滿足了，那麼能推出，不存在一個正確的隱變數定理。

後來，實驗觀察到了違背這個不等式的結果，所以，不存在一個正確的隱變數定理。

結論就是：
貝爾不等式的推翻說明了：不可能有任何隱變數定理能描述量子理論的不確定性，也就是說，量子的隨機性是真隨機，而不是因為我們探測水平有限而呈現的偽隨機。
低智商預警，本答案適合給基本不懂量子力學的人看，初中生完全能看懂，物理專業大學生以上會認為純屬廢話。

————————————————————

如果有兩個光子A和B，當我們用方向相同的偏振片來檢測它們的偏振態時，AB總是給出相反的結果，我們就說A和B相互糾纏，AB是一個糾纏光子對。

我們從三個隨機選取的方向來測量它們的偏振態，這三個方向分別是垂直方向（x），與垂直夾角10度（y），與垂直夾角20度（z）。 Ax為+表示光子A可以通過垂直方向的偏振片，Ax為-表示光子A不能通過垂直方向的偏振片，其餘類推。

由於A和B相互糾纏，所以如果Ax為+，那麼Bx必然為-，其餘類推。

現在假設隱變數理論是正確的，就是說一個光子能否通過一個特定方向的偏振片並不是概率性的，而是確定的，由一個未知的變數M來決定。
對於一個糾纏光子對AB，必有MA=-MB，從而保證了光子A能通過一個特定方向的偏振片時，B不能通過。

現在我們將所有M可能的取值分為8組，分別標記為{M1}{M2}{M3}{M4}{M5}{M6}{M7}{M8}。

分組遵循以下原則：

當MA∈{M1}時AxAyAzBxByBz為+++---，該組光子占所有光子的比例設為N1。

當MA∈{M2}時AxAyAzBxByBz為++---+，該組光子占所有光子的比例設為N2。

當MA∈{M3}時AxAyAzBxByBz為+-+-+-，該組光子占所有光子的比例設為N3。

當MA∈{M4}時AxAyAzBxByBz為+---++，該組光子占所有光子的比例設為N4。

當MA∈{M5}時AxAyAzBxByBz為-++--+，該組光子占所有光子的比例設為N5。

當MA∈{M6}時AxAyAzBxByBz為-+-+-+，該組光子占所有光子的比例設為N6。

當MA∈{M7}時AxAyAzBxByBz為--+++-，該組光子占所有光子的比例設為N7。

當MA∈{M8}時AxAyAzBxByBz為---+++，該組光子占所有光子的比例設為N8。

由於M是未知的，我們不可能知道的M的取值，而且我們也無法對同一個光子的偏振態測量三次，所以我們並沒有辦法測量N1到N8具體的值，所以囉嗦了這麼多，其實還沒有到重點。

下面我們來定義一個新的參數：相關度P，Pab表示在a方向測量A，在b方向測量B，如果AaBb總是正負相同，那麼Pab=1，叫做AB正相關，如果AaBb總是一正一負，那麼Pab=-1，叫做AB負相關，如果AaBb正負相同和一正一負的次數一樣，那麼Pab=0，叫做AB完全不相關。 這個相關度P就是貝爾不等式的關鍵了。

顯而易見，對於糾纏光子對，ab如果相互平行，那麼Pab=-1，ab如果相互垂直，那麼Pab=1。那麼如果ab不平行也不垂直，Pab該如何表示呢？只要用正相關的概率減去負相關的概率就可以了。

現在我們來把Pxy，Pzy和Pxz分別用N1到N8表示出來：

Pxy=-N1-N2+N3+N4+N5+N6-N7-N8

Pzy=-N1+N2+N3-N4-N5+N6+N7-N8

Pxz=-N1+N2-N3+N4+N5-N6+N7-N8

然後我們找出這三個相關度之間的關係：

Pxz-Pzy=-2N3+2N4+2N5-2N6

=2（-N3+N4+N5-N6）

| Pxz-Pzy |=2|-N3+N4+N5-N6|

=2|N4+N5-N3-N6|

=2|（N4+N5）-（N3+N6）|

由於N1到N8都是≥0的數，對於≥0的數來講，|a-b|≤|a+b|，所以

2|（N4+N5）-（N3+N6）|≤2|N4+N5+N3+N6|

即| Pxz-Pzy |≤2|N4+N5+N3+N6|

由於N3N4N5N6都是≥0的數，

所以|N4+N5+N3+N6|=N3+N4+N5+N6

所以| Pxz-Pzy |≤2（N3+N4+N5+N6）

由於N1+N2+N3+N4+N5+N6+N7+N8=1

所以

2（N3+N4+N5+N6）

= 1-N1-N2-N7-N8+N3+N4+N5+N6

=1+Pxy

所以| Pxz-Pzy |≤1+Pxy

這就是大名鼎鼎的貝爾不等式了。

是不是超簡單？所以廣大民科朋友們，千萬不要氣餒！拿起強大的初中數學武器，就可以和那些高高在上的所謂科學家們作戰了！誰說初中數學不管用了，貝爾不等式就是！哈哈哈（此段人格分裂中）

驗證貝爾不等式的實驗有很多，均證明量子力學是違反貝爾不等式的，也就是說我們推出貝爾不等式所用的假設隱變數理論是錯誤的。

但這只能說線性局域隱變數理論是錯的，並不能說非線性和非局域隱變數理論不對，這兩個理論太複雜，我們暫時不討論（實際上是我還沒搞明白）。

另外，我們上面所討論的糾纏光子對，是負相關的，其實也可以有正相關的糾纏光子對，在對貝爾不等式的驗證實驗中最出名的一個，阿斯派克特實驗，裡面使用的糾纏光子對就是正相關的，但這並不影響貝爾不等式的結論。


一些基礎的抽象問題

1）貝爾不等式究竟是在闡述一個什麼問題？其論證的邏輯是怎樣的？最終的結論又是什麼？

貝爾不等式闡述定量刻畫量子糾纏的關聯函數的性質。在某種隱變數模型下，假設隱變數按照經典概率分布，系統的關聯函數的之間存在一個上限。(比如自旋bell是關聯函數之差有一個上限)

2）根據貝爾不等式，什麼事情是「理應受其限制」而不可能發生的呢？

3）阿斯派克特的實驗究竟在邏輯上是怎麼證明貝爾不等式是不成立的？
關聯函數的實驗值破壞貝爾不等式(超出上限)。

4）阿斯派克特的實驗究竟是說明了什麼又否定了什麼？

說明存在某些量子糾纏態在類空間隔下具有非經典關聯。有很大的可能局域隱變數模型不能解釋量子力學表現出的概率行為。量子力學很可能是非定域的。

為什麼不能下結論？因為Bell不等式有一些隱含的假設(實驗setting 無關...)。
一些反對意見比如參見Superdeterminism。另請參考Superdeterminism的反對意見。

這個問題似乎還沒有完全定論因此可能最後回答沒有大家那麼肯定。。
逐條回答吧：

1）貝爾不等式究竟是在闡述一個什麼問題？其論證的邏輯是怎樣的？最終的結論又是什麼？

貝爾不等式 |Pxz-Pzy|≤1+Pxy 闡述了以下一個問題：

EPR佯謬：對於一個粒子衰變產生的兩個單態自旋反向運動的粒子，他們在理論上應該具有相反的自旋方向，
這個觀點
經典物理和量子力學觀點都是一致的
（這裡經典物理指的是指認為量子力學應該也是「定域」和「實在」的，即不存在超距關係，和存在著獨立於我們觀測的外部世界）
（這裡量子力學觀點是指非定域和非實在）

但所不同的是，根據量子力學的觀點，在觀測之前，兩者自旋是處於不確定的疊加態之中（糾纏態），兩者不可分離（無論相隔多遠），只有測定了其中一個粒子的自旋方向，另一個粒子的自旋方向才能確定
而經典物理認為，從衰變分離的那刻開始，兩者的自旋都是確定的。而兩者的區別可以由貝爾不等式區分。
定域實在的經典物理必須滿足貝爾不等式因為他們認為兩個粒子無法交換信息，這個式子是他們相關性的極限，
而量子力學之下 則不需要滿足，因為兩者從產生後就不可分離，相關性很強，只有在測量後，波函數塌縮，我們才能確定兩者自旋方向，而不同方向的測量跟測量方式相關，因此相關性和概率不是線性的（經典情況）而是連續的。

其中不等式的含義：Pxz代表觀測A粒子在x方向和y方向自旋同向的相關性（在大數統計時亦或認為是其概率），式子其餘同。
其推導邏輯有點複雜，我引用一下 曹天元《上帝擲骰子嗎-量子力學史話》裡對貝爾不等式的推導過程（我個人認為他的解釋是最簡潔的），並做了些排版，供參考：
我們用一個向量來表示自旋方向，現在甲乙兩人站在遙遠的天際兩端等候著A和B的分別到來（比方說，甲在人馬座的方向，乙在雙子座的方向）。
在某個按照宇宙標準時間所約好了的關鍵時刻（比方說，宇宙歷767年8月12日9點整，聽起來怎麼像銀英傳，呵呵），兩人同時對A和B的自旋在同一個方向上作出測量。
那麼，正如我們已經討論過的，因為要保持總體上的守恆，這兩個自旋必定相反，不論在哪個方向上都是如此。假如甲在某方向上測量到A的自旋為正（＋），那麼同時乙在這個方向上得到的B自旋的測量結果必定為負（－）！

換句話說，A和B——不論它們相隔多麼遙遠——看起來似乎總是如同約好了那樣，當A是＋的時候B必定是－，它們的合作率是100％！
在統計學上，拿稍微正式一點的術語來說，（A＋，B－）的相關性（correlation）是100％，也就是1。
我們需要熟悉一下相關性這個概念，它是表示合作程度的一個變數，假如A和B每次都合作，比如A是＋時B總是－，那麼相關性就達到最大值1，
反過來，假如B每次都不和A合作，每當A是＋是B偏偏也非要是＋，那麼（A＋，B－）的相關率就達到最小值－1。當然這時候從另一個角度看，（A＋，B＋）的相關就是1了。
要是B不和A合作也不有意對抗，它的取值和A毫無關係，顯得完全隨機，那麼B就和A並不相關，相關性是0。
在EPR里，不管兩個粒子的狀態在觀測前究竟確不確定，最後的結果是肯定的：在同一個方向上要麼是（A＋，B－），要麼是（A－，B＋），相關性是1。
但是，這是在同一方向上，假設在不同方向上呢？假設甲沿著x軸方向測量A的自旋，乙沿著y軸方向測量B，其結果的相關率會是如何呢？
冥冥中一絲第六感告訴我們，決定命運的時刻就要到來了。

實際上我們生活在一個3維空間，可以在3個方向上進行觀測，我們把這3個方向假設為x，y，z。它們並不一定需要互相垂直，任意地取便是。每個粒子的自旋在一個特定的方向無非是正負兩種可能，那麼在3個方向上無非總共是8種可能（把每個方向想像成一根爻，那麼組合結果無非是8個卦）。
x y z：+ + +，+ + -，+ - +，+ - -，- + +，- + -，- - +，- - -。

對於A來說有8種可能，那麼對於A和B總體來說呢？顯然也是8種可能，因為我們一旦觀測了A，B也就確定了。如果A是（＋，＋，－），那麼因為要守恆，B一定是（－，－，＋）。
現在讓我們假設量子論是錯誤的，A和B的觀測結果在分離時便一早註定，我們無法預測，只不過是不清楚其中的隱變數究竟是多少的緣故。
不過沒關係，我們假設這個隱變數是H，它可以取值1－8，分別對應於一種觀測的可能性。
再讓我們假設，對應於每一種可能性，其出現的概率分別是N1，N2……一直到N8。現在我們就有了一個可能的觀測結果的總表：
Ax Ay Az Bx By Bz 出現概率：

+ + + - - - N1
+ + - - - + N2
+ - + - + - N3
+ - - - + + N4
- + + + - - N5
- + - + - + N6
- - + + + - N7
- - - + + + N8
上面的每一行都表示一種可能出現的結果，比如第一行就表示甲觀察到A在x，y，z三個方向上的自旋都為＋，而乙觀察到B在3個方向上的自旋相應地均為－，這種結果出現的可能性是N1。因為觀測結果8者必居其一，所以N1＋N2＋…＋N8＝1，這個各位都可以理解吧？
現在讓我們運用一點小學數學的水平，來做一做相關性的練習。
我們暫時只察看x方向，在這個方向上，（Ax＋，Bx－）的相關性是多少呢？我們需要這樣做：當一個記錄符合兩種情況之一：當在x方向上A為＋而B同時為－，或者A不為＋而B也同時不為－，如果這樣，它便符合我們的要求，標誌著對（Ax＋，Bx－）的合作態度，於是我們就加上相應的概率。
相反，如果在x上A為＋而B也同時為＋，或者A為－而B也為－，這是對（Ax＋，Bx－）組合的一種破壞和抵觸，我們必須減去相應的概率。

從上表可以看出，前4種可能都是Ax為＋而Bx同時為－，後4種可能都是Ax不為＋而Bx也不為－，所以8行都符合我們的條件，全是正號。

我們的結果是N1＋N2＋…＋N8＝1！所以（Ax＋，Bx－）的相關是1，這毫不奇怪，我們的表本來就是以此為前提編出來的。如果我們要計算（Ax＋，Bx＋）的相關，那麼8行就全不符合條件，全是負號，我們的結果是－N1－N2－…－N8＝－1。

接下來我們要走得遠一點，A在x方向上為＋，而B在y方向上為＋，這兩個觀測結果的相關性是多少呢？現在是兩個不同的方向，不過計算原則是一樣的：要是一個記錄符合Ax為＋以及By為＋，或者Ax不為＋以及By也不為＋時，我們就加上相應的概率，反之就減去。
讓我們仔細地考察上表，最後得到的結果應該是這樣的，用Pxy來表示：

Pxy＝－N1－N2＋N3＋N4＋N5＋N6－N7－N8
嗯，蠻容易的嘛，我們再來算算Pxz，也就是Ax為＋同時Bz為＋的相關：

Pxz＝－N1＋N2－N3＋N4＋N5－N6＋N7－N8
再來，這次是Pzy，也就是Az為＋且By為＋：

Pzy＝－N1＋N2＋N3－N4－N5＋N6＋N7－N8
好了，差不多了，現在我們把玩一下我們的計算結果，把Pxz減去Pzy再取絕對值：

|Pxz－Pzy|＝|－2N3＋2N4＋2N5－2N6|＝2 |N3＋N4－N5－N6|
這裡需要各位努力一下，超越小學數學的水平，回憶一下初中的知識。關於絕對值，我們有關係式|x－y|≤|x|＋|y|，所以套用到上面的式子里，我們有：

|Pxz－Pzy|＝2 |N3＋N4－N5－N6|≤2（|N3＋N4|＋|N5＋N6|）
因為所有的概率都不為負數，所以2（|N3＋N4|＋|N5＋N6|）＝2（N3＋N4＋N5＋N6）。最後，我們還記得N1＋N2＋...+N8＝1，所以我們可以從上式中湊一個1出來：

2（N3＋N4＋N5＋N6）＝1＋（－N1－N2＋N3＋N4＋N5＋N6－N7－N8）
看看我們前面的計算，後面括弧里的一大串不正是Pxy嗎？所以我們得到最終的結果：

|Pxz－Pzy|≤1＋Pxy
這個不等式有深刻的含義。
在經典解釋下，觀測不影響一開始分離出來粒子自旋的相關性，無論方向怎麼取，量子力學隱含什麼隱變數，只要它是局域的，內在的相關性必然限定在貝爾不等式範圍內，而且相關性是分立線性的，只有那麼些可能。
但是在量子力學體系下，因為A和B是一體的，在某種特定的觀測條件下（比如x和y方向的夾角θ很小，換句話說cos θ很大），兩者會體現很強的相關性，會突破貝爾不等式的限制，而且相關性是連續的（與觀測角θ相關）。

最終的實驗結果（80年代之後有很多實驗，而非僅僅只有一個），基本上支持了量子力學的觀點，即量子力學是非定域和非實在的。
但目前也有部分科學家也認為現有的實驗存在「偵測漏洞」、「通訊漏洞」等實驗漏洞，對貝爾不等式提出了質疑。但量子通信等實驗對貝爾不等式有側面的支持。

2）根據貝爾不等式，什麼事情是「理應受其限制」而不可能發生的呢？

貝爾不等式是針對經典物理中對量子力學必須具備=的」定域性「和」實在性「兩個觀點進行了證偽。如果兩者是成立的，在其限制之下，A和B的波函數是獨立的（聽起來這似乎是更加直觀和正確），並無存在瀰漫全空間的」糾纏態「波函數，也無超距相互作用和觀測引起的"實體變化"
"糾纏態"被證明是存在的，但它與所謂"超距相互作用"是有本質區別的。

量子力學的非定域性並不支持信息的超距傳播。"糾纏態"本身是一個整體，無論A、B相距多遠。在測量時兩者的塌縮雖然是"瞬時"的，但兩者並未交換任何信息，從資訊理論角度，兩者「共擔」了整個量子態的信息，或是嚴格意義上說A、B是不可分離的（雖然從距離上是分離的，我指的是量子態上）。
在量子通信中，處於糾纏狀態的兩個粒子雖然表面上會對對方的測量作出"瞬間"反應，但是要把另一個粒子信息傳播回來還需要經典信道，因此也不存在超距的量子通信。

3）阿斯派克特的實驗究竟在邏輯上是怎麼證明貝爾不等式是不成立的？

阿斯派克特的實驗由鈣原子單次躍遷中同時發射的反向運動的光子對進行偏振測量以檢驗貝爾不等式。因為光子是無質量粒子，其自旋為1，只有兩個自由度，對應光子的兩個偏振方向。
A、B兩個光子反向遠離後，對A粒子的自旋進行x、y兩個方向的測量（x、y非正交，而且為了統計效果經常在變化），測量的方法是不停改變光子偏振方向。
對B粒子也進行相同的測量。
這樣得到了四個偏振方向的測量結果Ax、Ay、Bx、By。
根據貝爾不等式，如果現實是定域性的，則關聯函數（關於兩邊四個檢測器分別對應四個偏振角度上同時檢測結果的函數Ax，Ay，Bx，By）的值必須介於一定範圍之間而不能突破。
但是，所有的實驗結果均表明：貝爾不等式不成立，
在一定統計下，關聯函數會超越局域隱變數所預計的最大區間，而且，關聯函數的值分布總是符合量子理論（採用糾纏態波函數描述光子）的預測，測量結果跟觀測角度方向相關，是連續而非線性的。
因此，現實是非定域性的，而且可以被量子理論描述。

4）阿斯派克特的實驗究竟是說明了什麼又否定了什麼？

一句話：說明了量子力學是非定域的非實在的，糾纏態被證明是存在的，在測量之前，糾纏態中的粒子波函數不是獨立存在的而是不可分離的，否定了愛因斯坦有關量子力學必須是定域實在的觀點。
證明了你我看到的現象有相關性，但又否認了獨立於你我之外存在的客體（沒有隱變數）。
直覺或者思維方式說如有相關必存在獨立客體，這是唯物主義的方法論。
不存在獨立客體必存在你我可以自由構造的主觀體驗並施加給第三者，這是唯心主義的推論。
兩個都是錯的。
沒有獨立存在的客體，卻存在著強關聯，舉例，月亮在我沒看的時候不確定是否存在，但你看到了我就有極大概率看到，雖然月亮這個客體並不存在，但你我之間還是相通的。
在量子力學出現之前，我們人類的所有概率觀念，都來自於已知條件的缺少，否則根本不存在概率的問題。
比如說，扔骰子，如果精確知道骰子質量分布，初始速度，空氣阻力等因素，那麼點數是可預知的，根本不存在不確定性。愛因斯坦認為，量子現象的概率性，也是如此。貝爾不等式，否定了這種看法。量子力學的概率性，是內稟屬性，和經典概率現象完全不同。這是一個實驗觀測的結論。

關於內稟屬性的解釋
：任何試圖用宏觀的規律去理解微觀現象，幾乎都是徒勞的。這也是量子力學很難有直觀的解釋和理解的原因。
所謂內稟屬性，是指量子力學的概率性，是微觀世界的一種屬性，和宏觀世界的概率性完全不同的起源。這個解釋有點車軲轆話了。
或者這麼說，量子力學之中的概率性，迄今為止沒有任何的解釋，是量子力學的基本假設之一，這個假設完全來自於觀測實驗，而不是來自於任何理論或者模型。
這種內稟的概率性，說的既不是粒子，也不是位置，也不是動量，說的是微觀＂粒子＂本質上是一種瀰漫整個時空的概率波。
所謂位置，動量等宏觀量，都只在觀測意義上有定義。
有些科學家認為貝爾不等式的推導過程存在錯誤，當然也不可能用來判定量子力學的非定域性


對於量子力學的「測量必然影響被測量的物質」的說法，愛因斯坦叫了一些人過來提出EPR佯謬（EPR是愛因斯坦、波多爾斯基和羅森這三個人的名字的第一個字母的組合），對量子力學發起了挑戰：

「要打架了？算我一個！」

兩個系統在發生了相互作用後分開，測量其中的一個系統，得知其屬性之後，也就知道了另一個系統的屬性。如果根據量子力學的說法的話，測量其中的一個系統，也會影響另一個系統。這似乎表明存在超光速聯繫。在愛因斯坦看來，超光速聯繫是不可能的。以此，他認為量子力學並不是完備的理論，它還有有待發掘的東西。

因此，人們引入「隱變數」來解釋量子力學。所謂的「隱變數」就是人們尚未知曉的物理量。

而貝爾不等式說明了任何一個「隱變數」理論，都不能概括量子力學的全部內容。也就是，「隱變數」理論是無法解釋量子力學的，它不能解釋量子力學的全部內容。

不過，貝爾不等式只是否定了定域性的隱變數理論，但並未否定非定域性的隱變數理論。

阿斯派克特的實驗的精確性具有決定性意義，它和量子力學符合得相當好，而和貝爾不等式的偏差相當大。

剩下的問題，你可以在對貝爾不等式的簡單易懂的推導中找到答案。

這得從愛因斯坦-玻爾爭論開始說起。
簡單來說
1.愛因斯坦等提出EPR佯謬，指出量子力學的哥本哈根詮釋是不完備的。量子力學正確，但是不是一個完整的理論，可能是另一個更好理論的近似，量子力學不能完整的描述世界。
玻爾的反駁是：量子力學具有非局域性，所以EPR佯謬不正確，而量子力學是完備的。

2.物理學家假設EPR佯謬是正確的，假設存在一種新的理論可以完全的容納量子力學，只是需要在量子力學的基礎上增加額外的未知參數來描述完整的解釋世界。未知參數用隱變數表述，所以稱為「完備的」隱變數理論。
舉個例子，相對論對於牛頓經典力學。

3.數學家馮諾依曼，做個一個證明，具體什麼我忘了。
而後貝爾提出了貝爾不等式，
重點來了：貝爾不等式的意義在於，假如愛因斯坦是正確的，存在隱變數理論，那麼實驗結果滿足貝爾不等式，否則玻爾正確。它提供了一種實驗方法和理論，可以驗證EPR佯謬的正確性。

那麼問題答案來了
1.以上已經回答，這就不重複了
2.假如實驗結果滿足貝爾不等式，量子力學的非局域性就不成立，量子隱形傳輸等等都不會存在
3.這個實驗就是根據貝爾的理論進行的 一種可操作性的實驗，貝爾不等式原來的理想實驗是電子。
4.這個實驗的意義就是貝爾不等式的意義，不重複了。

(0) Bell不等式和糾纏不是等價關係；Bell不等式和糾纏都是用來表徵多體相關，簡單常見的就是兩體（bipartite correlation）。 違背Bell不等式的correlation一定糾纏，但是糾纏不一定違背Bell不等式。

(1)Bell不等式其實有兩個定理。1964年最著名的那個定理：自然中存在某些量子現象與局域性和決定論（locality and determinism）這兩個假設不兼容。其中決定論這個概念等價於predetermination，realism（所謂的現實主義），隱變數理論。 1976年的定理：自然中存在某些量子現象與局域因果律（local causality）不兼容。 有一部分物理學家和大部分哲學家混淆了局域性和局域因果律，所以會根據Bell不等式得出不同的結論。

(2) Bell不等式首先根據1976的定理說明局域因果律應該被拋棄，這是我們唯一的選擇。但是根據1964年的定理，我們有兩個選擇：保留局域性，拋棄決定論，即承認絕對的隨機（量子保密通信和密碼的基礎），這是大部分物理學家的觀點；保留決定論，拋棄局域性。由於部分人把局域因果律當成局域性，所以拋棄局域性便是順理成章，即支持非局域性（nonlocalist）。

(3)局域性用稍微通俗的語言解釋：兩個空間無論隔離多遠的兩個物體A和B， A的測量結果（outcomes）應該與B的選取怎麼測量，即選取實驗設置無關（setting）。局域因果律：兩個空間無論隔離多遠的兩個物體A和B， A的測量結果（outcomes）應該與不僅與B怎麼測量，即選取實驗設置無關（setting），而且也與B的測量結果無關。 局域性可以由愛因斯坦的相對論因果律（relativistic causality）直接推導出來，所以拋棄局域性意味著拋棄相對論因果律。

(4)阿斯派克特的實驗證明了滿足Bell不等式的量子相關存在，而不是純粹理論的概念，即women需要做出自己的如(2)的選擇。但是阿斯派克特的實驗存在探測效率漏洞（efficiency loophole），因為其實驗結果可以人為的被隱變數理論構造出來。
否定了局域隱變數的存在


如果你不看月亮時，月亮真的有可能不存在。
這些天研究了貝爾不等式，嘗試著表達自己粗淺的認識。
從百度百科有貝爾不等式的推導過程。推導過程中假設了什麼，那麼最終否定的必定是假設的內容。
Ax Ay Az Bx By Bz 出現概率：

+ + + - - - N1
+ + - - - + N2
+ - + - + - N3
+ - - - + + N4
- + + + - - N5
- + - + - + N6
- - + + + - N7
- - - + + + N8
N1+N2+N3+N4+N5+N6+N7+N8=1
以上這些就是推導過程中所假設的內容。測試結果是貝爾不等式被打破，就是證明了這些假設是錯的，N1+N2+N3+N4+N5+N6+N7+N8不等於1。