前面曾提過，z0..z1..z2..cycle這種曲線，MetaPost是使用貝茲曲線所繪出的。貝茲曲線是現代電腦繪圖重要應用，較詳細內容，可以考維基百科內的說明。MetaPost手冊內提到，它是使用3次方貝茲曲線，也就是指，z1..z2中間的曲線，是由二個參考點所算出的路徑。它的數學式，是

p(t)=(1-t)^3p_0+3t(1-t)^2c_0+3t^2(1-t)c_1+t^3p_1, t為[0,1]間的任意數

這個算式中，t 是 0到1中間的任意數，而z1..z2這條曲線就是這些t值所算出的點的集合，因為點p_0, c_0, c_1, p_1是已知的值，所以是t的一元三次方程式的圖形。在曲線path的計算中，這個t值十分的重要，之後的許多工作，都是從它開始。

不是數學家、程式專家，這都不要緊。了解貝茲曲線公式的意義，之後的繪圖工作中，才能有效運用MataPost所提供的運算元，對曲線作出正確的計算，達成我們所要繪出的效果並不會太因難。

前面的公式，只是z1..z2二個點（一個弧，arc）的計算，一個貝茲曲線可以經過無數個點，如是經過3個點，則其t值會在0到2中間的任意數。而t=0時，會在起點z1；t=1時，會在中間點z2；t=3 時，會在終點z3；如果是z(n), 則t 會在 0到n-1之間。運算元point of提供了以t值算出path上面的點（pair)為何。

point (t) of path; t是數值變數。計算結果是pair值。

但如果是環狀的封閉曲線path時怎麼辦呢？那不是沒有終點或起點了嗎？t值可能對應到任何path上的位置。MetaPost提供了這個運算元length，它可以算出path有幾個弧。

length(path)；算出path有幾個弧。如果有3個弧，那只要計算0到3之間的t值就可以了。

另外，還有subpath of的運算元，可以把path拆開，分成不同的弧的path。

subpath (t pair) of path；這裡的pair是t值的pair，（t1, t2)，就是把path中的t1值所對應的點，到t2值所對應的點，這二點中間的路徑被輸出成為新路徑。其結果值是path。如果t1>t2，則結果路徑會是原路徑反向的路徑。

和subpath of相近的另一個運算元，為cutafter, cutbefore。path a, b; 

a cutafter b; 的意思就是a path 把和 b 的交叉點後的path 切去，其意思等同於

subpath (xpart(a intersectiontimes b), length(a)) of a;

a cutbefore b; 就等於是

subpath (0, xpart(a intersectiontimes b)) of a; ( intersectiontimes 等一下會討論，它的意思是求二個path交點的t值，因為有二個path，所以其值是一個 t pair，（t1, t2), t1是前path交點的p值，t2為後path在交點的t值。）

direction (t) of path; 這是重要的運算元，它可以提供path在t值時的path的向量。在畫切線必備。

directiontime (direction vector) of path; 這也很好用的，求出path 的在某方向量的t值。

directionpoint (direction vector) of path; 一樣，可以算出path在某方向量時的點。

Metapost也提供了和length相似的運算元，arclength

arclength(path)；傳回一個數值，是arc length。如果 a 是 0到 arclength(path)中間的值，則

arctime a of path; 傳回一個t值，則

arclength(subpath (0, t) of p)=a;

postcontrol (t) of path; 算出path 在t值時的後控制點（pair)。

precontrol (t) of path; 算出path在t值時的前控制點 （pair)。

計算二個path交點的運算元(path1) intersectiontimes (path2)；p1, p2為二個path，a intersectiontimes b; 可以得一個t 值的 pair (t1, t2), 則t1是p1在交點的t值。t2是在p2在交點時的t值。如要求交點坐標，則可以用 point (t1) of p1; 在MetaPost 手冊中有提到，如果有二以上的交點時，p1 intersectiontimes b; 只能算出其中的一個點，如果要把所有的點都算出，則要用subpath of 等把path切開分別計算。如果無交點，則會傳回(-1, -1)的值。

(path1) intersectionpoint (path2); 運算結果是一個pair，為二path的交點。

這個例子是t值在曲線path的繪圖應用：

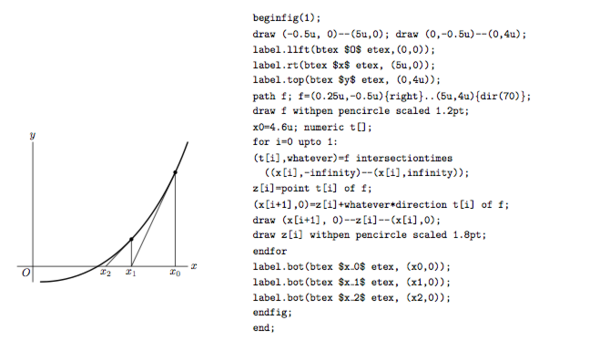
這個例子，是牛頓逼近法的示意圖，使用interseciontimes求出t值再做圖，裡面使用了一個常數infinity，為數值的最大值4096：

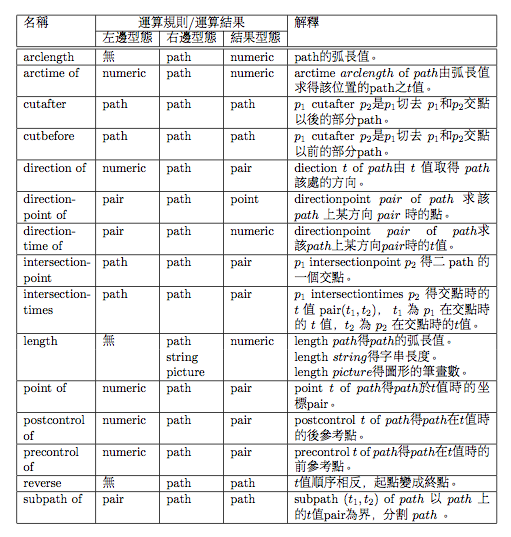
 最後，以上這些曲線path運算元，都可以應用在直線path上面，因為直線也是一種沒有曲線的曲線。以下是相關運算元表：