任意三等分角(自創) - johnson324 的網誌

字體：小中大

任意三等分角(自創)

2010/11/22 10:48:32瀏覽871｜回應0｜推薦1

分享一個關於任意三等分角的自己想出的一個解法, 應該也是違反只能用無標記直尺與圓規命題標準. 好玩就好.

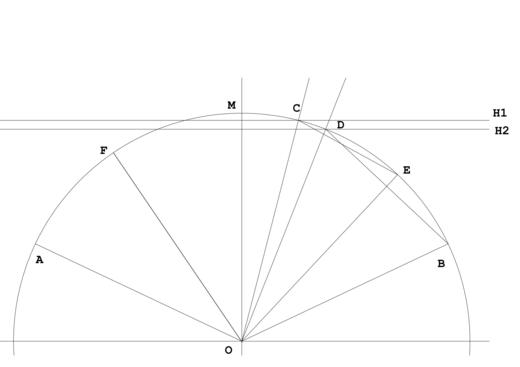
如圖: 角AOB為一任意角, OM為平分角AOB的平分線.

1. 在OM間選擇一點, 畫水平線H1, 交圓於點C.

2. 由點C往點B方向畫割線, 交圓於點E. 使角MCO=角ECO

3. 將水平線H1往下移動, 當水平線到H2位置, 點E重合點B, 點C重合點D, 此時角DOB=1/3角AOB.

此圖有一個很好玩的性質, 當點E尚未重合點時, 角COD=1/3角EOB.

另外相對的來說, 假設角AOB為已知可3等份的特殊角如90度角, 藉由調整H1與H2的距離, 可以獲得許多不同非特殊角FOE的1/3之一角COE.

( 創作｜其他 )