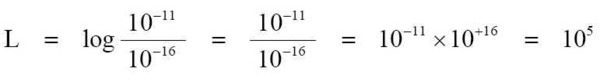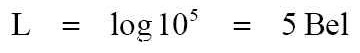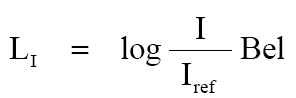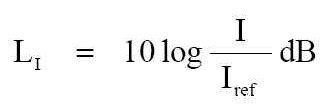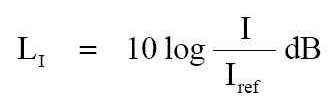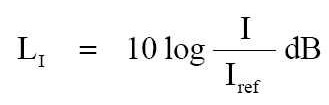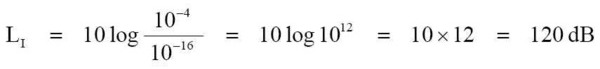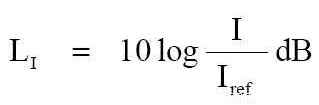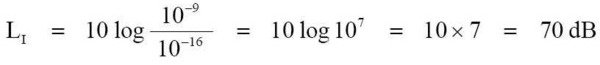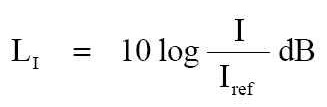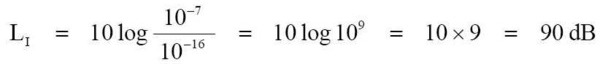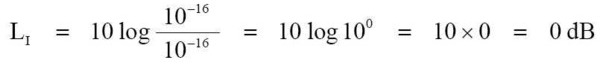字體：小 中 大 |
|
|
||||||||||||||||||||
| 2015/02/13 14:45:16瀏覽716｜回應0｜推薦0 | ||||||||||||||||||||
貳拾柒、聲學強度位準 (再解釋 dB-1) ※這篇是從『再解釋 dB-1』轉過來的。 --- 如果我們以動態範圍 ( dynamic range ) 來說，動態範圍是最大聲的聲音強度到最小聲 ( 最安靜 ) 的聲音強度之比值 ( 比率 ) 。 如果我們以電氣聲學系統來說，這動態範圍是系統所能夠生產出或者是在可容許接受的沒有失真或者沒有傷害到我們人類耳朵聽覺的聲音強度大小。 例如以在放大器的電子組件的參數來說，這在最大的情況是所能夠生產出的最大聲的聲音，條件是要正好在低於過荷 ( 過載 ) 所造成變形的失真電平位準之下。 另外還有個最小的情況，就是該裝置的「自有噪音」電平位準的層級部分。 任何比較小聲的聲音，應該是超出並掩蓋住了那由機器或系統內部所產生的自有噪音。 --- 我們人類的耳朵是很奇妙的裝置。 它們有個動態範圍從最安靜的 10-16 W/cm² (或 10-12 W/m² ) 的可聽聞感覺聲音強度延展到在耳朵正好對某聲學位準產生疼痛和傷害之下的最大聲之聲學聲音位準。 這個最大響度是發生在 10-4 W/cm² (或 100 W/m² ) 的強度。所以人類耳朵的動態範圍是 10-4 到 10-16 ，這動態範圍即是「1012」。 這量額數值是「1 兆」 ( 兆 = T 、 Tera- 、 Trillion ) ，這是在 1 之後有 12 個阿拉伯數字的「0」 ( 零 ) ，即是「1,000,000,000,000」。 --- 據說比一個合乎標準規格的人造音響機器還要多達百萬倍。 人類耳朵的動態範圍超過了最好的放大器的動態範圍，這最好的放大器的動態範圍是起碼要有「1010」。 人類耳朵的動態範圍比一台性能良好的放大器之動態範圍還要超出百倍。 由於我們人類耳朵聽覺具有這樣巨大的動態範圍之原因，聲音強度以 10 ( log ) 的指數去量測比起用線性刻度的數目字去表示來說，這是更方便與更合適不過的了。 --- 因此早在上個世紀初，貝爾實驗室的科學家們就創造出基礎於利用指數的對數 ( logarithm ) 之聲音測量與計值單位。 這個聲音的測量單位是「Bel」 ( 貝爾 或 貝 ) ，這 Bel ( B ) 是等於一個聲音強度指數去對應個聲學參考強度的比率。 參考的強度位準是我們人類聽覺所能聽到的最低「閾」值是 10-16 W/cm² 。 註：這「閾」 讀音為「ㄩˋ」與「域」的讀音發音相同；英文是「threshold」；臨界、界限、限界、定限、臨限、門限、門檻；上限/下限、高限/低限、等等的意思。 --- 因此，假如量測到個聲音強度是 10-11 W/cm² ，就要把這聲學位準去與聲學參考值作照會比較。 請參閱下面的這式子：
在上面的式子中之「L」在此是表示「強度位準」 ( intensity level ) 。 --- 聲學的位準 ( level ) 通常是以大寫的「L」英文字母去表示。 而聲學位準有許多種不同的，這就衍生出在大寫的 L 之後委附於下標的字母去表示。 例如：
表格 15 、 幾個聲學位準 再解釋 dB-1_tab-1 --- 強度位準是這樣去求取的：
式子中的： ◾ LI 是強度位準，單位為 Bel ◾ I 是強度，單位為 W/cm² ◾ Iref 是參考強度，單位為 W/cm² 在實際使用的慣例上，必須要用個比較小的單位值，因此要將這 Bel 除以 10 的十分之一貝爾。 貝爾的十分之一是 分貝 ( decibel 、 dB ) ，簡寫與符號是「dB」。 我們都是使用與利用這「dB」單位，這樣的強度位準就成為下面的式子：
--- 例題 1. 如果有個 10-7 W/cm² 的聲音，請問這 10-7 W/cm² 以 dB 值的強度位準是多少呢？ 公式：
帶入數據：
01_eq-06 去解這式子： 1. (10-7) － (10-16) = 10-9 2. 把「－」號轉換成「＋」的值， 10-9 成為 109 3. 這 109 是 1,000,000,000 ，轉換成 log 是 9 4. 答案： LI = 10 × 9 = 90 dB --- 在前面所提到的，我們人類耳朵的聽覺在 10-4 W/cm² 以上的強度位準是會會使得耳朵聽覺受傷的。 假設這 10-4 W/cm² 的強度位準是我們人類耳朵的最高聽覺極限，而如果在這數據還算是安全的話。 例題 2. 請問這 10-4 W/cm² 是多少 dB 呢？ 公式：
01_eq-07 帶入數據：
01_eq-08 去解這式子： 1. (10-4) － (10-16) = 10-12 2. 把答案的「－」號轉換成「＋」的值， 10-12 成為 1012 3. 這 1012 是 1,000,000,000,000 ，轉換成 log 是 12 4. 答案： LI = 10 × 12 = 120 dB --- 例題 3. 如果有個 10-9 W/cm² 的聲音，請問這 10-9 W/cm² 以 dB 值的強度位準是多少呢？ 公式：
01_eq-09 帶入數據：
01_eq-10 --- 例題 4. 如果有個 10-7 W/cm² 的聲音，請問這 10-7 W/cm² 以 dB 值的強度位準是多少呢？ 公式：
01_eq-11 帶入數據：
01_eq-12 --- 在前面所提到的，我們人類耳朵的聽覺能從最安靜的 10-16 W/cm² 的可聽聞感覺聲音強度。 假設這 10-16 W/cm² 的強度位準是我們人類耳朵的最低聽覺極限。 例題 5. 請問這 10-16 W/cm² 是多少 dB 呢？ 公式：
01_eq-13 帶入數據：
01_eq-14 ---
|
||||||||||||||||||||
| ( 知識學習｜科學百科 ) | ||||||||||||||||||||
