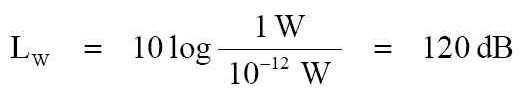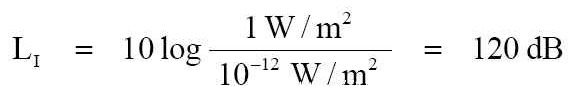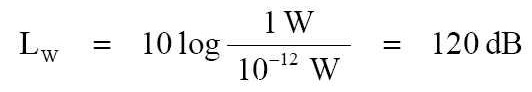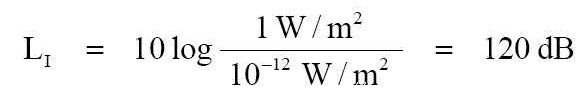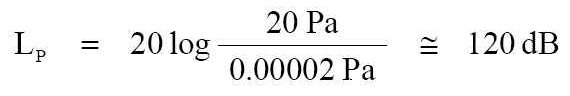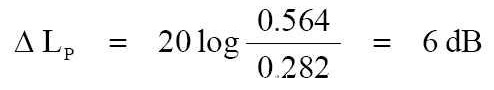參拾貳、簡述聲音的傳播

※這篇是從『簡述聲音的傳播-1_20030221A』轉過來的。

===

簡述聲音的傳播-1

在物理學上來說，聲音是一種能量。

針對於物理學分科的聲學方面而言，聲波 (sound wave ；音波) 是從個聲學音源裝置放射發出的，這些聲學音源裝置是處於環境大氣壓力下與空氣的調制 (調變； modulation) 過程所產生出的聲波。

---

在電氣聲學 (electro-acoustical) 及聲音增援 ( sound reinforcement, SR) 系統方面，我們用揚聲器去取代那個聲學音源裝置當成個聲學音源時；當輸入了功率電能去驅動揚聲器時，揚聲器是把輸入的功率電能轉換成機械動能以振動的方式去壓擠空氣分子相互地振動再產生出聲能波形。

---

點音源

所謂的「點音源」 (point source) 是在空間中的個聲學裝置被假設為 1 個點，是當這聲學裝置被驅動在空間中時所放射出的聲音。

而所謂的「真實點音源」其實說的是具有無窮小尺寸的，因為是先以「點」為訴求，也就是說是個抽象的想法和在實際上是不可能去實現的。但這卻不會妨礙到我們把這概念用於去描述在實際上所可實現的裝置之特性方面。

假如點音源在效率上是完美的話，而如果對它輸入個 1 電力瓦特的功率就會產生出 1 聲學瓦特放射聲能的能力。這是如果沒有產生造成熱消耗所能完全做到的，因為使得所有的電力都轉變成機械動力、和聲學功率了。從這音源所放射出的能量是從此音源向四面八方均等的運動移動向外。

---

指向定向 (directional) 的能量放射是以「干涉」脫出的波去完成的。因為真實的點音源是全方向性 (omni-directional) 的，所以對於為了要指向定向就要去做干涉式的導引，因此就需要有一個干涉的物體存在著。 (註：在此將不會述說有關於干涉的影響效應。)

如果把1 pW ( pico-Watt = 10^-12 ) 利用來當作為個功率參考值，如此地由聲學裝置以 1 聲學瓦特所生產出的「聲音功率位準」 (或聲能級； sound power level) 將是：

(eq1)

注意：這聲音功率的定義，在此不涉及音源距離。這 L_W ＝ 120 dB 是表示所可能產生於 1 瓦特電功率之最高的聲音功率位準。事實上在我們地球這真實世界所有的裝置都缺乏能力將放射不到那想要的距離處，因此它們必需要被額定於效率和功率的耗散 (dissipation；消耗、漏泄、散逸、消散) 比率。

---

現在我們要選擇個觀察點，這觀察點是在距離聲音音源 0.282 公尺遠的地方。之所以選擇這個距離，是為了方便起見而選取的距離。

由於隨著聲音能量的傳播，這就形成個球形的球面波之波陣面。如果這個波陣面以 0.282 公尺來說，就將有個 1 平方公尺的表面積。

如此這樣地 1 瓦特的輻射聲音功率就經過 1 平方公尺的表面積。

(eq2)

這是音源之聲音強度位準 (sound intensity level) 和表示穿過個球體表面 1 平方公尺的功率之數額(量值)。而且這是以全方向裝置所可能做到 100% 效率的最高強度位準。不像 L_W 、 L_I 一般(樣)的能夠巧妙的由局限處理放射能量到較小的面積範圍。

由在個點所觀察到的，這作用所獲得的位準效益是叫作「指向性指數 DI」(方向性指數； directivity index)，並是用分貝來表示表達的。

所有的揚聲器為了配合聲音增援就必須要犧牲指向性控制來換得到這實效。

---

對於所描述的理想裝置，球表面的 L_P 將在數目上是與 L_W 和 L_I (L_P ＝ 120 dB) 相同的，因為由 1 瓦特所生產出的聲音壓力將是 20 Pa 。

這個 L_P 只是針對於在球上的一個點而已，但是因為點音源是全方向的，這在這個球上的所有點都將是相同的。

---

再次扼要的說明，在這點音源遠方的 0.282 公尺處，聲音功率位準、聲音強度位準、及聲音壓力平方的位準在數目字上將是相同地。

(eq3)

(eq4)

(eq5)

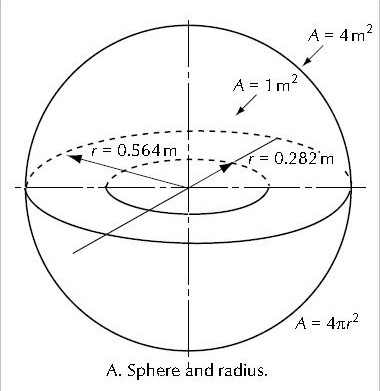
圖 4 、這個條件形成標準的術語學的基礎並用來描述從揚聲器聲音放射的關係。(此圖取材自 Don and Carolyn Davis, “Sound System Engineering” 2nd edition 1989, page 44, figure 3-6(A); Howard W. Sams & Co. )

---

平方反比定律

我們現在再去觀察那距離音源有兩倍遠的個點。隨著波繼續傳播展開來，在它半徑的 0.564 公尺之總面積以 0.282 公尺而言，將是乘以 4 這個面積。當聲音運動移動往兩倍的遠處時，這傳播所展開的覆蓋是乘以 4 這個面積。

以分貝來說，從第一點到第二點的聲音位準之變化是：

(eq6)

在圖 4 所表達的這種方式叫作「平方反比定律」 (inverse square law, ISL) 。由於放射出的波是以球形的方式傳播展開的；對於一個點音源放射器而言，因此表示出平方反比定律所描述的位準衰減與距離的對比。

由於將會受到了大氣吸收導致對所依據取決之頻率損失，但在這裡我們暫不考慮這些，暫時忽略掉這些問題。

多數的揚聲器大致上能概略地在從音源遠離位準變化於依隨平方反比定律。

---

在圖 5 所述說的是， s 為音源位置處，當使得距離音源的距離再增加倍至 2r時，所放射聲音能量將遍佈兩倍的這個面積。由是 L_I 和 L_P 將下落 6 dB 。

圖 5 、對於指向定向的裝置而言，依據平方反比定律在該裝置的遠程位置處的遠場 (far field) 也是如此地。 (圖取材自 維基百科_Inverse-square law http://en.wikipedia.org/wiki/Inverse-square_law#mediaviewer/File:Inverse_square_law.svg )

◾ 亦可參考 Google Search_搜尋圖片搜尋結果 https://www.google.com.tw/search?q=inverse+square+law&tbm=isch&tbo=u&source=univ&sa=X&ei=wwHbVP2xFNKB8QWR-YLgAQ&ved=0CCYQsAQ&biw=960&bih=1419&dpr=1.25

---

---

   網際網路資源：

◾ Tonstudiotechnik – Sengpielaudio_『Sound intensity I and the inverse square law 1/r²』 http://www.sengpielaudio.com/calculator-squarelaw.htm

---

◾ Crown Audio_『Inverse Square Law Calculator』 http://www.crownaudio.com/inverse-square-law.htm

---