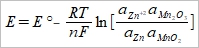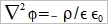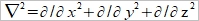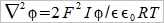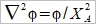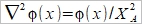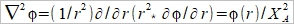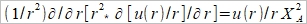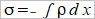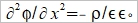字體:小 中 大
字體:小 中 大 |
|
|
|
| 2017/12/28 22:05:33瀏覽2711|回應0|推薦0 | |
Metallurgical electrochemistry textbook: Electrochemistry, Philip H. Rieger, Prentice-Hall 為什麼兩個金屬接觸會有電流, 電壓? ⸪Fermi energy level redistribution Ex. Na 1s²2s²2p⁶3s¹ Zn-Cu system: half reaction Zn →Zn²⁺+2e +) 2e+Cu²⁺→Cu Zn+Cu²⁺→Zn²⁺+Cu 化學反應伴隨電能的改變, energy change
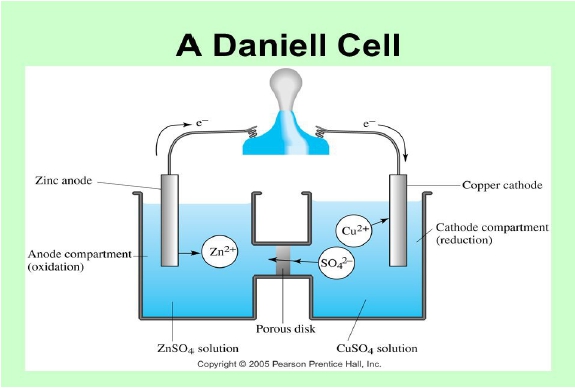
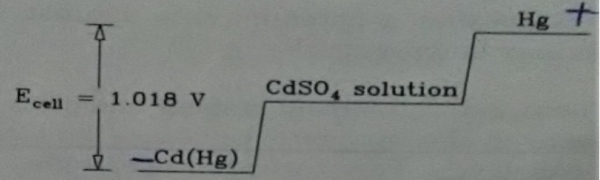
∆u=q-w 能量不滅,Zn-Cu system要符合第一定律 w=P∆V+wₑₗₑ+mdH-γdA, γ: surface tension, 表面積增加, system能量愈大→w減少 q=TdS, S: entropy, 商 ∆u=TdS- P∆V-wₑₗₑ(dH=0, dA=0), at constant P, ∆u+ P∆V=∆H ⸫∆H=TdS-wₑₗₑ ⸪∆H-T∆S-S∆T=∆G, if constant T, ∆T=0 ∆G=-wₑₗₑ if spontaneous reaction, wₑₗₑ=”+”, → Zn+Cu²⁺→Zn²⁺+Cu ∆G=”-” 表示Zn-Cu system對外界做正功, ⸪∆G=-wₑₗₑ wₑₗₑ=QE, ∆G=-QE= -nFE, F=96485 coul/equivalent, n: valence value E=”+”, 若電位為正,表示是”spontaneous reaction”. notation: Zn|Zn²⁺||Cu²⁺|Cu E=”+” Cu|Cu²⁺||Zn²⁺|Zn E=”-” n=equivalent/mole, F=96485 coul/equivalent Daniel cell: Zn|Zn²⁺||Cu²⁺|Cu, Weston cell: Cd(Hg)|CdSO₄||CdSO₄• Hg₂SO₄|Hg₍ₗ₎ Cd →Cd²⁺+2e anode(anodic reaction) +) Hg₂SO₄+2e→2Hg+SO₄²⁻ cathode(cathodic reaction) overall Cd+ Hg₂SO₄→2Hg+Cd²⁺+SO₄²⁻ ∆G= -nFE half cell define: hydrogen reference H₂→2H⁺+2e “E=0” +) Cd²⁺+2e→Cd 半電池電壓 H₂+Cd²⁺→2H⁺+Cd ECd²⁺/Cd (1) Cu²⁺→ Cu ECu²⁺/Cu (2) (2)-(1) Cd+Cu²⁺→Cu+Cd²⁺ E= ECu²⁺/Cu- ECd²⁺/Cd 可以視反應為redction or oxidation reaction, 再做加減 ∆G⁰(J/mole)= -nFE⁰, E⁰:volt, F=96485 coul/eq Weston cell: standard cell Cd(Hg)|CdSO₄₍ₛ₎|CdSO₄₍ₛₒₗ₎|Hg₂SO₄₍ₛ₎|Hg₍ₗ₎ 25℃ E=1.018V potentiometer ∆G⁰= -nFE⁰=-2×96485×1.018, 如何知道n=?, 寫出half cell reaction 2e+Cd²⁺→Cd Ecd²⁺/Cd (1) Hg₂SO₄+2e→2Hg₍ₗ₎+SO₄²⁻ EHg₂SO₄/Hg₍ₗ₎ (2) (2)-(1) Cd+ Hg₂SO₄→2Hg+Cd²⁺+SO₄²⁻ E⁰cell=EHg₂SO₄/Hg₍ₗ₎- Ecd²⁺/Cd=1.018V
standard potential, E⁰ : 1M= 1 mole solute per 1 Kg of solvent, ex. 1 mole [Cd²⁺] or [SO₄²⁻] ⸪∆G⁰= -RTln(aHg²acd²⁺aSO₄²⁻/aCdaHg₂SO₄) p.s. aX+bY→cW+dZ, K=[aXᵃaYᵇ/aWᶜaZᵈ]⁻¹ ∆G=∆G⁰+RTln(aHg²acd²⁺aSO₄²⁻/aCdaHg₂SO₄) 除以-nF, ∆G/-nF=∆G⁰/-nF+RTlnK/-nF → E= E⁰-(RT/nF)lnK or E= E⁰-(0.0592/n)logK at 25℃ ai=γiXi → a=γiCi (mole → molar) Applicaton of half cell reaction m× A+ne→B E⁰A/B E有per electron 的意思 -) n× C+me→D E⁰C/D mA+nD→mB+nC E⁰cell= E⁰A/B- E⁰C/D ∆G⁰A/B= -nFE⁰A/B, ∆G⁰C/D= -mFE⁰C/D → ∆G⁰cell=m×∆G⁰A/B-n×∆G⁰C/D= -mnFE⁰A/B+ nmFE⁰C/D= -nmF(E⁰A/B- E⁰C/D) ⸪∆G⁰cell=-nmFE⁰cell ⸫E⁰cell=E⁰A/B- E⁰C/D p.18 ex. Pt₍ₛ₎|I⁻₍ₐq₎I₂₍ₛ₎||Fe²⁺₍ₐq₎Fe³⁺₍ₐq₎|Pt₍ₛ₎ anodic I₂₍ₛ₎+2e→2I⁻₍ₐq₎ E⁰I₂/I⁻=05355V cathodic Fe³⁺+e→Fe²⁺ E⁰Fe³⁺/Fe²⁺=0.771V overall cell 2Fe³⁺+2I⁻→2Fe²⁺+ I₂ E⁰cell=0.2355V ∆G⁰= -nFE⁰=-45.4 KJ/mole = -RTlnK= -RTln(aFe²⁺²aI₂/aFe³⁺²aI⁻²) K=exp(-∆G⁰/RT)=8.6×10⁷≈[Fe²⁺]²/[Fe³⁺]² → [Fe²⁺]/[Fe³⁺]≈1×10⁴ 用來做測量K很準確 ex. Ag⁺₍ₐq₎+e→Ag₍ₛ₎ E⁰=0.7991V...(1), AgBr₍ₛ₎+e→Ag₍ₛ₎+Br₍ₐq₎ E⁰=0.0711V...(2) (2)-(1) AgBr₍ₛ₎→Br₍ₐq₎+Ag⁺₍ₐq₎ E⁰cell=0.0711-0.7991=-0.728V ∆G⁰= -nFE⁰=+70240 J/mole= -RTlnK, K=exp(-∆G⁰/RT)=4.87×10⁻¹³≈[Ag⁺]² ⸫[Ag⁺]=7×10⁻⁷
∆G₃⁰=∆G₁⁰+∆G₂⁰= -mFE⁰A/B-nFE⁰B/C → -(m+n)FE⁰A/C= -mFE⁰A/B-nFE⁰B/C ⸫E⁰A/C=(mE⁰A/B+nE⁰B/C)/(m+n) half → half 不能用addition ex. Fe³⁺+e→Fe²⁺ E⁰Fe³⁺/Fe²⁺=0.771V Fe²⁺+2e→Fe₍ₛ₎ E⁰Fe²⁺/Fe₍ₛ₎= -0.44V → Fe³⁺+3e→Fe₍ₛ₎ E⁰Fe³⁺/Fe₍ₛ₎=(0.771-0.44×2)/3= -0.11V Formal potential E=Eº-(RT/nF)ln(aprod./areact.)=Eº-(RT/nF)ln([prod.]γprod./[react.]γreact.)= Eº-(RT/nF){ln([prod.]/[react.])+ln(γprod./γreact.)}=Eº′-(RT/nF)ln(γprod./γreact.) i.e. Eº′=Eº-(RT/nF)ln([prod.]/[react.]) e.g. Na在HCl 和H₂SO₄的γNa值不同 Latimer diagram acid 2NO₃⁻+4H⁺+2e→N₂O₄+2H₂O Eº=0.8, ∆G⁰= -nFE⁰=-2F×0.8 ⸫ N₂O₄ more stable
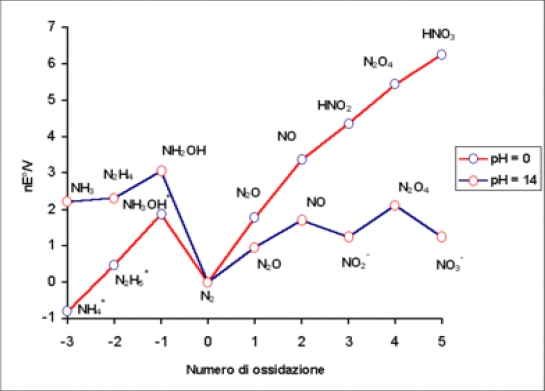
p.26 ∆G⁰-oxidation state diagram
NO₃⁻+3H⁺+2e→HNO₂+H₂O Eº=0.94V E=Eº-(RT/nF)ln(aHNO₂aH₂O/aNO₃⁻aH⁺³)= Eº+(3RT/nF)lnaH⁺=Eº+(3RT×2.303/nF)log[H⁺] =Eº-(3RT×2.303/nF)pH=Eº-(3/2)×0.0592pH i.e. pH= -log[H⁺] battery
primary
anode: Zn → Zn²⁺ + 2e⁻, cathode: 2MnO₂(s) + 2H⁺(or H₂O) + 2e⁻ → Mn₂O₃(s) + H₂O(or 2OH⁻) E=1.55V cell reaction: Zn(s) +2MnO₂(s) + H₂O → Zn²⁺ + Mn₂O₃(s) + 2OH⁻ (pH上升→NH₄OH緩衝溶液) Why irreversible? 1. form ZnO· Mn₂O₃ spinel stable, 2. form ZnO oxide → 短路 3. voltage will be lowered. 1.35~1.55V
anode: Zn²⁺ + 2OH⁻ → Zn(OH)₂↓ 『keep voltage constant”, but KOH more corrosive.
Zn(s)|Zn²⁺(aq), KOH(aq), Zn(OH)₂|HgO(s)|Hg(l) anode: Zn²⁺ + 2OH⁻ → Zn(OH)₂↓(or Zn(OH)₄²⁻) cathode: HgO(s) + H₂O + 2e⁻ → Hg(l) + 2OH⁻ 天冷時, T<10℃ → aZn(Hg)↓↓ ⸫E ↓↓
anode: Zn²⁺ + 2OH⁻ → Zn(OH)₂(s) cathode: ½ Ag₂O₂(s) + H₂O + 2e⁻ → Ag(s) + 2OH⁻ cell reaction: Zn(s) +½ Ag₂O₂(s) + H₂O → Ag(s) + Zn(OH)₂(s)
Secondary
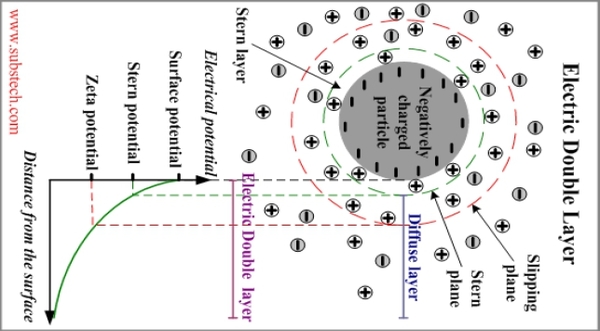
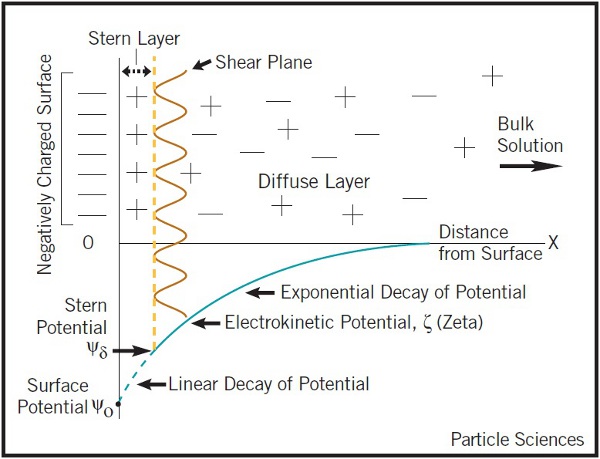
anode: Pb + SO₄²⁻ → PbSO₄(s) + 2e⁻ cathode: PbO₂ + 4H⁺ + SO₄²⁻ + 2e⁻ → PbSO₄(s) + 2H₂O cell reaction: Pb + PbO₂ + 4H⁺ + 2SO₄²⁻ → 2PbSO₄(s) + 2H₂O, [H₂SO₄]>2M→ E=2V a. PbSO₄ is porous, E will not decay. b. [H₂SO₄]↓ → E↓ c. DensityPbSO₄ < DensityPb, PbO₂ → expansion volume, 放電不能太激烈! d. 充電時, PbSO₄ → Pb + PbO₂ or may 2H⁺ + 2e⁻ → H₂ ↑ 遇火花爆炸, regulator控制充電電壓不讓H₂ 產生 電化學介面:電極與電解液的介面,用電雙層模型描述電解液介面的離子電荷分布; 電雙層亦即Helmholtz layer 加上Gouy layer.
Helmholtz layer: 被靜電吸引,固定在表面的離子, Gouy layer:靠近表面做布朗運動,游移擴散的離子; 此二種離子電荷相加, 去中和電極表面的電荷 電雙層的電位函數, ϕ(r) or ϕ(x) Poisson equation ϵ: 材料介電常數, ϵ₀:自由空間係數=8.854×10⁻¹²c²J⁻¹m⁻¹, ρ:空間電荷密度 運算子
ρ=ΣziFci ...(b) zi:離子電荷, ci:離子濃度, F:法拉第常數 探討電荷密度, ρ中的濃度ci, 利用Boltzman分布描述濃度與電位能之關係 Ni/N0=exp[-(Ei-E0)/kT] 電位能 Ei=zi eϕ at zi 位置, E0=0 遠離介面的電解液 所以 Ni/N0=exp(- zi eϕ/kT) 並且mole轉換成molar Ni= ci NA → ci/c0=exp(- zi Fϕ/RT) ...(c) i.e. e/k=eNA/kNA=F/R 將(c)代入(b) ρ=ΣziFc0exp(- zi Fϕ/RT) 再代入(a) Poisson-Boltzman equation ²ϕ= -(F/ϵ ϵ₀)Σzic0exp(- zi Fϕ/RT) ...(d) ⸫微分方程式的解即為電位函數ϕ(r) 冪級數表示 exp(u)=1+u+u²/2+u³/3+... as u << 1 因此當 zi Fϕ/RT << 1, → zi ϕ << RT/F (d)式可寫成 ²ϕ= -(F/ϵ ϵ₀)Σzic0[1- (zi Fϕ/RT)+½(zi Fϕ/RT)²-...]≈ -(F/ϵ ϵ₀)Σzic0[1- (zi Fϕ/RT)]= -(F/ϵ ϵ₀)Σzic0+(F²ϕ/ϵ ϵ₀ RT)Σzi²c0= (F²ϕ/ϵ ϵ₀ RT)Σzi²c0 i.e. Σzic0=0 電中性 ion strength defined by I= ½ Σzi²c0 ⸫ 式中的常數關係定義為 XA= (ϵ ϵ₀ RT/2F²I)½ → 一維 球座標模擬粒子周圍的電位分布 if ϕ(r)=u(r)/r 代入(e)
→(1/r²)∂/∂r[r²(-u(r)/ r²+u(r)/r)]=u(r)/rXA² → (1/r²)∂/∂r[-u(r)+u(r)]= u(r)/rXA² →(1/r²)[-u(r)+u(r)+ru(r)]= u(r)/rXA² → u(r)= u(r)/XA² 線性微分方程式 方程式解 u(r)=Aexp(r/XA)+Bexp(-r/XA)
u(r)=aϕaexp(a/XA)exp(-r/XA)=aϕaexp[(a-r)/XA] ⸫ ϕ(r)=u(r)/r=(a/r)ϕaexp[(a-r)/XA] r>a ….(f) 此結果為假設球表面, 也就是Helmholtz layer往外延伸的電位函數, 若以此函數描述電雙層:
Helmholtz layer是第一層(被靜電吸引,固定在表面)的離子,可視為由ϕs表面電位到ϕa(Helmholtz layer表面電位)呈線性分布 ϕ(r)=ϕs(1 -r/a)+ϕa(r/a) 0<r<a Gouy layer的擴散電位,可視為以(f)式的直角座標表示 ϕ(r)=ϕaexp[(a-r)/XA] r>a 表面電位ϕa與表面電荷密度之關係 整個系統保持電中性的狀況下, 淨表面電荷(包含Helmholtz layer)必須和Gouy layer的空間電荷取得平衡, 達成電中性
⸪ Gouy layer模型的弱點 (1)適用於稀釋溶液, 在比較濃的溶液中會有很大的誤差 (2)利用溶劑的平衡介電常數來計算短距的電力,其實受到表面電荷的水電偶,會使所在位置的電性變得與平衡時狀況很不一樣 所以定性上可以解釋, 但定量上不適用!! |
|
| ( 知識學習|隨堂筆記 ) |