最近在看書，看到關於飽和蒸氣壓的內容。

想當初高中化學沒好好念，一直沒搞懂飽和蒸氣的物理意義是什麼，現在可好了，看吧，書到用時方恨少，於是我只好乖乖地上網啃資料。

結果看了一晚上的網頁這才驚覺，原來課本上講的、大家所理解的，就和當初我囫圇吞棗的記憶沒什麼兩樣呀！什麼道爾頓、理想氣體分程式、亞佛加厥假說、同溫同體積的理想氣體分子數量相同，我甚至還記得 1 mole 有 6×1023個分子啊！是，沒錯，我是不會解題，但我記得的概念一樣沒少啊。

但重點不在於我知道什麼，而是我到底理解了什麼。我知道水的飽和蒸氣壓等於大氣壓時，水會沸騰；但我更想理解的是，為什麼水的飽和蒸氣壓等於大氣在時水會沸騰！

不是說網路上的文章沒有解釋，而是這些解釋太膚淺，一堆話繞了半天也就是「水的飽和蒸氣壓等於大氣在時水會沸騰」這句話的改寫，再不然就是一堆看似有理的理論，但講到後來卻又互相矛盾的文章。

所以，到後來我覺得，不是我高中沒學好，而是我想知道的東西沒教，因為，天殺的，你知道水會沸騰就好了，我已經告訴你這時飽和蒸氣壓等於大氣壓了，你還想怎樣？啊？

嗯，諸如此類，你知道的。

事到如此，只好靠自己了。

以下是我自己琢磨出來的，文長，想知道為什麼水在飽和蒸氣壓等於大氣壓時會沸騰但又沒耐心的人，可以拉到最下面，那兒有重點整理。

本文開始！

首先，在探討飽和蒸氣壓之前，先來看看氣體的壓力如何產生：

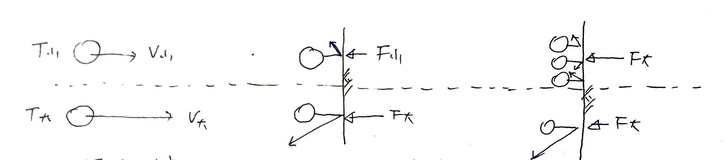
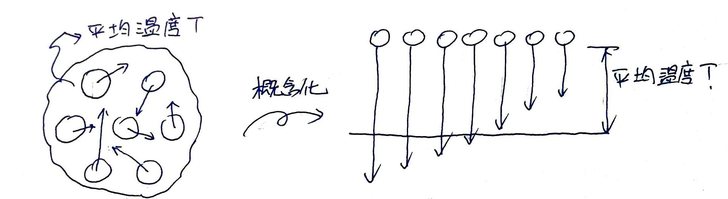
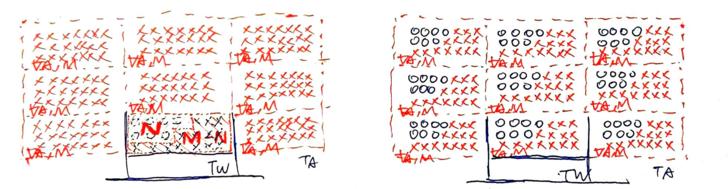
Fig 1. 密閉空間中，溫度T對 (a) 分子速度V與  (b) 施力F之影響，及(c)分子數量n對施F力之影響。

(a) T給予分子速度。

(b) 分子運動狀態改變（速度變化），起因為受力，施力來源為壁面。

(c) 要增加壁面受力，可增加撞壁的分子數量。

氣體的溫度T，來自其分子的運動速度V；即氣體中分子們的運動度速越大，則氣體的溫度越高（圖1.a）（這就是大氣增溫層的氣溫可以到四、五十度的關係吧）。

當氣體分子撞到壁面後（圖1.b），分子反彈而出現運動狀態的改變，這個改變來自於壁面的施力-F（定義向右為正）。壁面施給分子的力-F，其反作用力即為分子施給壁面的力+F，這個力施加在單位面積A上，即為該面積的壓強P。

（題外話，「壓強」在中文中更常叫作「壓力」，但壓力不是「力」，而是「單位面積的受力」；英文叫做pressure，也不是force。所以有人把pressure翻作「壓強」，個人覺得比壓力貼切多了） 。

要如何增加壁面單位面積上的受力（即壓強）P呢？從圖1.c中的上半部可看出，只要增加空間中的分子數量，則撞在壁面上的分子數量便會跟著增加，此時即便氣體分子速度V低（因溫度T低），但因同時有較多的分子在壁面上施力，壓強仍可以獲得提升，使其與圖1.c中下半部的壁面受力相同。

綜合上述，可知決定分子運動速度V的，不是壓強P（即壓力），而是溫度T，而壓強P僅是分子運動速度發生改變時（撞牆或水面）的副作用而已。

再來，一團溫度為T的氣體，當中的每個分子都具有不同的運動方向與速率（圖2.a），如果將其概念化，其結果則如圖2.b所示。

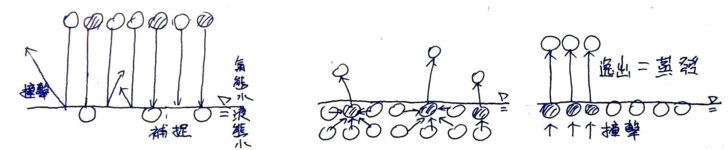
Fig2. 平均溫度為T的氣體團中，分子們的運動狀態。(a) 實際，(b) 概念化。

（題外話，這樣的概念化是有憑有據的，課本上說了，分子的運動速度V決定了溫度T，或是反過來亦可，但一團溫度為T的氣體，其每個分子的溫度Tm都一樣嗎？顯然不是。一團氣體中，分子速度有快有慢，如圖2.a所示。如果把實際的氣體分子運態狀態概念化，也就是讓分子們依速度V排排站好，其結果如圖2.b所示，此時可看出，在所有的分子中，有一部份的分子速度比平均值大，另一部份比平均值小，但平均起來就是平均速度V（廢話）。然而，前述說氣體分子的運動速度即可表示為溫度，因此圖2中，那團氣體的平均溫度T，即可用分子們的平均速度V來表示。也就是說，在一團平均溫度為T的氣體中，有一部份的分子運動速度比整體的平均速度V小，另一部份則比平均速度V大。)

這時候如果在圖 2.b的下方放置一堆液態水，會發生什麼情形？如圖3.a所示，圖中的分子們就是圖2.b中的分子們，有幾個就是運氣差到了一個極點，他們撞進水面時動能剛好被下方的液態水分子抵消，結果便無法反彈，最後只能停留在液態水中，換句話說，就是他們被補捉，也就是凝結了。

另一方面，液態水在水面附近的分子也正在發生相似的事：這些分子互相推擠，然後就這麼剛好，水面處有顆分子自己在往上衝的同時，又被臨近的水分子推了一把，於是他便如此這般地順勢離開水面，像個變心的女友再也回不來了（如圖3.b）。液態水分子透過這種方法逸出水面而成氣態水，就是蒸發的過程與原理，而該過程概念化的結果，則如圖3.c所示。

而圖3.a與圖3.b則分別為水的「微觀凝結」與「微觀蒸發」機制。

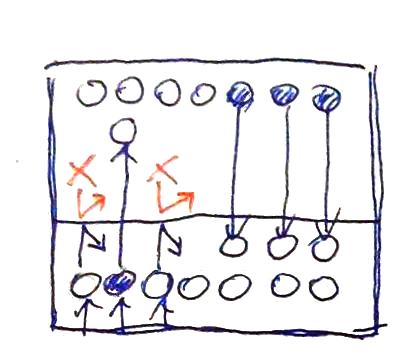
Fig 3. 水面補捉水分子，與水面分子逸出水面（即蒸發）。

(a) 空氣中，氣態水分子撞擊水面後無法反彈，被液態水面補捉。

(b) 液態水中，水面附近的分子互相撞擊，使少量水分子獲得能量，而逸出水面，即蒸發。

(c) 水蒸發概念圖。

以上都不是我話唬爛的，資料來源為《蒸氣壓| 科學Online – 科技部高瞻自然科學教學資源平台》：

液體靠近表面的分子，動能較大的會逃脫而進入氣態，然而逃脫分子也可能會與液體上方的氣體分子相碰撞，而使得有些分子重返液體內。密閉容器中，由液體逃脫的 分子越來越多，這些逃脫的分子也會碰撞到液體表面而被捕捉，這就出現凝結現象。

這裡講到一個重點，即從水分子的蒸發（逸出）到水分子的凝結，兩個過程中都只用水分子間的撞擊便能解釋了；而水分子撞擊的速度V來自於溫度T，因此，水分子逸出水面（蒸發）與被補捉而重回水面的速度，便只有溫度T有關，那飽和蒸氣壓E呢？蒸發、凝結，都沒用到飽和蒸氣壓E的大小啊！

所以，接下來就要進入飽和蒸氣壓E的正題了…。

在飽和蒸氣壓E的實驗中，課本（還有網路上的文章們）都是從密閉空間開始的。所以我們也來設計一個密閉空間的飽和蒸氣壓E實驗，請見圖4。

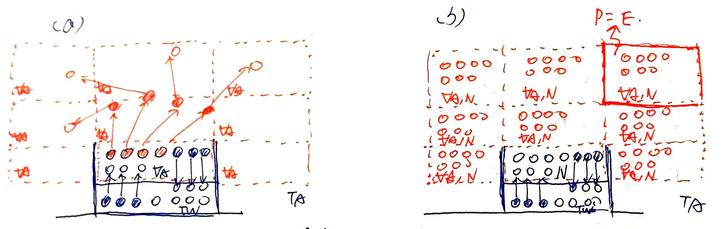
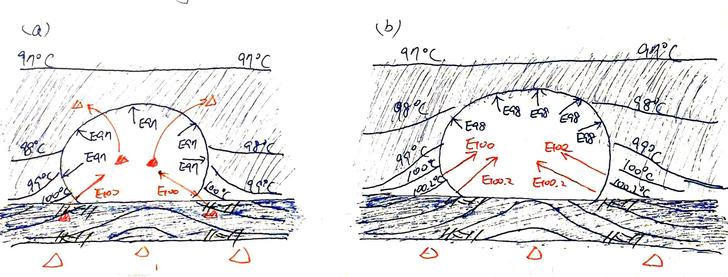
Fig 4. 密閉空間實驗：飽和水分子量

(a) 初始狀態，無擾動，無汽化核，故不沸騰，近似過熱水，只有蒸發。

(b) 密閉空間中無水分子，故只有水面的水分子大量逸出，而無補充，此時「蒸發>>凝結」。衝出水面的分子速率與水中相似，故密閉空間中開始出現溫度TA，且TA≒Tw

(c) 因水溫Tw不變，故水分子逸出水面的速率不變。但上方密閉空間VA 中，氣態水分子變多了，故有小部份分子被水面補捉，只是速率沒那麼快，因此，此時「蒸發>凝結」。

(d) 水溫Tw仍不變，故水分子逸出的速率亦不變，但密閉空間VA中水分子的數量達到一個程度，使補捉率等於逸出，此時不僅蒸發與凝結同時發生，且兩者速率還相同，即「蒸發=凝結」，巨觀的蒸發處於動態平衡狀態，而密閉空間VA中的水分子數量達到飽和（N）。

圖4.a為實驗的初始狀態，我們在一個密閉的箱子裡裝了一些水，水溫為Tw，且水體的數量夠大，使蒸發的降溫可忽略（蒸發會把水體中的熱量取走，故水溫下降是正常的，但這樣一來，整個概念模型就太複雜了，所以，這裡還是就讓水溫不變吧）；水上方的空間則為密閉的空間，體積為VA，初始狀態下是沒有任何氣體分子的（水分子數量n=0），即真空（密閉空間中的壓強P=0）。為了簡化實際的變數，我們將這些水設定為沒有擾動，也沒有汽化核，換言之，他們安靜又乾淨，因此即便在真空下，水也無法沸騰，有點像過熱水一樣（沸騰與過熱水請容後再述，這裡就先當作真有這回事吧…）。

實驗開始後（圖4.b），因為無法沸騰，所以實驗初期僅有水面的水分子，透過逸出而蒸發到上方的密閉空間中。同時，上方的密閉空間因為幾乎沒有氣態水分子，因此便沒有水分子可透過補捉而凝結回水體中，即「蒸發>>凝結」，故水的體積快速減少，且巨觀的蒸發率（定義為「逸出水分子量-捕捉水分子量」，或「微觀的蒸發量-凝結量」）即為水面水分子逸出的速率。此外，由於密閉空間中的水分子來自於逸出水面的水分子，故其分子速度應與其在水裡時的分子速度相似，故當密閉空間中出現水分子後，該空間中便有了溫度TA，且TA≒Tw。

到了實驗中期（圖4.c），已有一定程度的水氣分子進入密閉空間VA中了，由於實驗之設定使蒸發時的降溫不甚明顯，故此時水溫應仍保持為Tw，而前述水分子逸出水面的速度僅受水溫Tw控制，所以水分子逸出水面的速度不變。然而，密閉空間中已然容納了不少溫度亦為TA的水分子，則其凝結回水面的速率變大；即水面同時發生蒸與凝結的行為，只是凝結的速度略慢罷了。故此時巨觀的水面蒸發率（實際的蒸發 - 實際的凝結）便逐漸降低。

實驗終了後，水溫Tw不變，故水面之水分子逸出速度仍和實驗開始時相同，但因水面上方的密閉空間中塞了不少溫度TA的水分子，多到其凝結回水面的速率與逸出的速率相同。此時蒸發與凝結仍然同時發生，只是速度想同因此巨觀的蒸發率便歸零了（實際的蒸發 - 實際的凝結=0，即蒸發與凝結達到動態平衡），換句話說：此時密閉空間VA中的水分子數量已達到飽和，無法再容納更多的水分子了！（再多也只是重新凝結回去）

這些也都不是我瞎編的，資料來源為《蒸氣壓| 科學Online – 科技部高瞻自然科學教學資源平台》：

當汽化和凝結過程均以同一速率進行即平衡達成時，蒸氣中的分子數目將不會改變，此時液體呈現的蒸氣壓稱為飽和蒸氣壓，溫度越高飽和蒸氣壓越大。

只是該死的，整個過程仍是只用水分子逸出與補捉就能解釋，況且讓逸出速度增加的是水溫，而不是壓力；決定無法讓巨觀蒸發率再增加的，則是密閉空間中的水分子數量達到飽和。而這兩項因素都還是與密閉空間中的飽和蒸氣壓無關啊。

換言之，飽和蒸氣壓可能只是水分子數量飽和的結果，而不是原因、機制，因此相要飽和蒸氣壓來解釋蒸發、沸騰（飽和蒸氣壓等於大氣壓時）等現象，看起來就是拿機制的結果來討論原因，想當然爾只會走進雞生蛋、蛋生雞的無限迴圈中。

所以回過頭來，到底什麼是飽和蒸氣壓？前面說過了，在密閉空間的實驗中，讓巨觀蒸發率達到平衡的，是密閉空間中的水分子數量達到飽和了，換言之，就是密閉空間中VA的水分子數量達到水分子飽和數量N，則水體不再蒸發更水分到密閉空間中（即巨觀的蒸發停止）。

所以現在我們在密閉空間中VA中有水分子飽和數量N，其溫度則是TA（≒水溫Tw），剛好我們還有個公式叫做理想氣體方程式：

P V = n R T

其中P是一團體積為V、分子數量為n的氣體，在溫度為T時的壓力，R則為常數。

我們已知的資料（V=VA, n=N, T=TA）代入理想氣體方程式可得：

E VA = N R TA，則 E = (N R TA) / VA！

其中N是密閉空間VA中、溫度為TA的水分子飽和數量，此時我們已然滿足理想氣體方程式裡四個未知數（P, V, N, T）的三個，所以一定能知道密閉空間中的氣體壓強P！密閉空間中的氣體是什麼？不就是達到飽和數量的水蒸氣分子嗎，所以氣體壓強P便可稱作水蒸氣的飽和蒸氣壓E了！

因此，結論就是，在密閉空間中的飽和蒸氣壓實驗，使蒸發達到動態平衡的，是「密閉空間VA中溫度為TA的水蒸氣分子數量」達到飽和數量N，則此時密閉空間VA中所對應的氣體壓強P即為飽和蒸氣壓E，得證。

也就是說，飽和蒸氣壓E並不是拿來解釋蒸發、沸騰的工具，而是從原理解䆁蒸發後的副產品。不過這個副產品好用，因為我們不知道飽和水分子數量N到底是多少（1 mole = 6×10^23個，慢慢數吧），但幸好壓力很好測，再者，這個壓力又可以代表飽和水分子數量N，所以用飽和蒸氣壓E來代表飽和水分子數量N，何樂而不呢？

所以當一個空間VA中水氣的飽和蒸氣壓是E，從蒸發的角度來看，更應該將這個蒸氣壓E看做空間VA中可以飽和時的水分子數量標誌N，這個N值不會侷限空間中的分子數量M，因為N只是某個數量的分界。也就是說，若空間VA中水分子數量M比N小，表示空間中的水分子數量未達飽和，蒸發會持續發生，並使空間中氣態水分子數量上升到N為止；空間VA中水分子數量M比N大，則表示空間中的水分子數量已然超過飽和狀態，氣態水分子會凝結回到液態，使空間中氣態水分子數量下降到N。

綜合上述，在指定的水溫Tw下，水體有一個飽和蒸氣壓E，若上方的體積為VA的空間中，含有溫度TA與水溫Tw相同水蒸氣，則透過E、TA與VA即可換算出空間VA中的飽和水蒸氣分子數量N。這個N值（對應一個E值）是個標誌，標著空間VA中的飽和界限在哪，但無法侷限空間中的水蒸氣分子數量M。舉例來說，飽和飽和水蒸氣分子N（對應一個蒸氣壓E）就像是高速公路上的速限110公里，但有人要超速（M>N）你攔不住他，有人龜速慢行（M

所以，在瞭解了飽和蒸氣壓E的義意後，現在便能進一步來看看，如果把密閉空間的蓋子打開會發生什麼事。

為了簡化問題，我們先讓密閉空間VA中的巨觀蒸氣壓E達到平衡，也就是圖4.c中的狀態（其中TA=Tw），再將整個箱子般到真空中，然後打開蓋子…，結果應該會像圖5.a中的情況。

Fig 5. 在真空的大氣中打開密閉空間的蓋子。

(a) 大氣為真空，原本在密閉空間中的水分子跑到整個開放的空間中。

(b) 除非原本的密閉空間VA中的水分子數量達到飽和水分子數量N，否則水體的蒸發不會停止。而若要將原本的密閉空間VA中的水分子數量達到飽和水分子數量N，則在箱子外面，每個體積為VA的空間，都要容納N個水分子。

原本箱子裡的密閉空間VA裡擠了N個水分子，使該空間的水分子數量飽和。但當箱子的蓋子打開後，原本的密閉空間VA旋即成為了開放空間VA，因此水分子得以暢行無阻離開開放空間VA。同時，因外界的空間是真空的，即外界的空間裡沒有水分子，於是便不會有外界的水分子回到開放空間VA。結果就是水體的水分子不斷逸出水面並進入開放空間VA中，然後水分子又立刻逸出到外界的真空中。

上述的擴散作用使得水面上方的空間VA一直無法達到飽和狀態（空間VA中的水蒸氣分子數量M等於飽和數量N），故水體的水分子只好不停地逸出到原本的密閉空間VA中，設法讓上方的空間達到水分子的飽和數量，直到液體水全部蒸發完畢， 或是…。

或是像圖5.b那樣，逸出的水分子總算填塞了外界每個體積為VA的空間，使當中的氣態水分子數量都達到飽和水分子數量N。此時，不僅氣態水分子離開與進入開放空間VA的速率相同，且開放空間VA中的氣態水分子數量亦達到飽和數量N。如此一來，開放空間中便有足夠的氣態水分子，使水分子被補捉進入水體中（凝結）的速率，等於水體水分子逸出水面（蒸發）的速率，然後水面的巨觀蒸發便停止了。

而這個狀態，其實就等於把整個真空的大氣都視為密閉空間，而這個大空間中，每個小空間VA中都塞滿了溫度為TA、數量達到飽和分子數量N的氣態水分子，亦即大氣飽和了。

這時候，如果我們在外界中任選一塊體積等於VA的空間（如圖5.b右上角那塊），計算出裡面的水分子數量（前面提過了，是飽和數量N），透過 P VA = N R TA （TA仍然等於水溫Tw）可知，該空間中的水蒸氣壓強P即為飽和蒸氣壓E（因為N是溫度為TA的空間VA中，所能容納的最大水分子數量）；又氣態水分子在整個大氣中是均勻分佈的，所以整大氣的壓強P，就是會水蒸氣的飽和蒸氣壓E。

前述這個模型是比較簡化的，因為初始假設大氣為真空。那如果一開始就把大氣中填滿空氣分子會怎樣呢（當然，不會填入水分子）

Fig 6. 在壓強為 1 atm、氣溫為 TA 的大氣中打開密閉空間的蓋子。

(a) 蓋子打開的瞬間，概念化成盒內空間VA中原有的水氣分子暫不移出，大氣分子先進入盒內，使盒內空間VA的壓強達到1 atm。此時，大氣中沒有水氣分子。

(b) 隨著水蒸氣分子由水體蒸發進空盒內空間VA，再擴散到大氣中，直到大氣都含有水分子飽和數量N之後，巨觀的大氣擴散停止，盒內空間VA的水氣分子數量終於達到飽和數量N，故水面巨觀的蒸發停止。然而，此時外界大氣的水氣分子數量亦達到飽和數量N，於是，整個大氣的含水量也飽和了。

壓強為 1 atm、氣溫為 TA 的大氣在體積為VA的空間中，可容納M個大氣分子。

根據亞佛加厥假說，壓強為 1 atm、氣溫為 TA 的大氣在體積為VA的空間中，只能容納M個氣體分子，故當體積為VA的空間中塞進N個水分子後，該空間便只能再容納M-N個大氣分子。此時氣溫為 TA 、體積為VA的空間中，水分子數量為飽和數量N，仍可計算出一個飽和蒸氣壓E，E比 1 atm 小，不足的部份由M個大氣分子補足（道爾頓分壓定律）

首先，我們把圖4.c中的箱子搬到壓強PA為 1 atm、溫度為TA = Tw 的大氣中，然後，打開蓋…等等！打開蓋子前，我們是不是應該先算一下體積為VA的空間中，若裝入了壓強為 1 atm、溫度為TA的大氣後，應該會有多少個大氣分子。

所以，幸好，根據理想氣體分程式 P V = N R T可知，一但指定了空間的體積（VA）、壓強（P）與氣體溫度（TA），那麼該空間中的大氣分子數量便是定值，所以，我們就叫這個定值為M吧。

再來這個M值，會比溫度為TA、體積為VA的飽和水分子數量N少嗎？查表可知，水的飽和蒸氣壓在溫度為攝氏0~50度時約為0.006 ~ 0.122 atm 間（都小於 1 atm），換言之，在一般的常見的室溫下（且氣溫等於水溫時），水的飽和蒸氣壓E都小於大氣壓PA。再者，一但指定了壓強（PA、E）、溫度（TA）與體積（VA）後，則體積為VA的氣態分子數量即是定值，故在沸騰前， 1 atm 的大氣分子數量M，必然會大於氣態水分子的飽和分子數量N。

其次，一個體積為VA空間，充滿了壓強為 1 atm、 溫度為TA的大氣分子，其分子數量應為M。此時，若要再空間VA中塞入N個氣態水分子，但仍要保持同樣的壓強與溫度，則此時空間VA中到底可以有幾個氣態水分子與大氣分子？

幸好亞佛加厥說了：

同溫、同壓時，同體積的任何氣體含有相同數目之分子。

因此可知，空間VA中的氣態水分子與大氣分子總和仍是M，但我們在空間VA中塞進了N個氣態水分子，故剩下的空間便只能容納 M-N 個大氣分子了。

所以現在我們可以打開蓋子了。

圖6.a顯示了打開蓋子後的情形。首先，因為打開蓋子前的密閉空間VA中只有N個溫度為TA的氣態水分子，但我們知道體積為VA的空間，應該容納M個溫度為TA、壓強為1 atm  的氣體分子。所以我們可以如此概念化：在蓋子打開的瞬間，先讓但外界溫度為TA、 1 atm 的大氣分子進入盒子中，此時盒子中VA的的空間已經裝了N個氣態水分子，所以進入盒子的大氣分子數量便只有M-N個。

之後，就如同圖5.a一樣，圖6.a中，盒子以外的空間都沒有氣態水分子，只有盒子裡的空間VA有N個，於是盒子裡的氣態水分子只好不斷地往大氣中逸出，這讓盒子裡的水分子數量從N快速向下減少，並讓水面上方空間VA中的水分子數量處於未飽和的狀態。這時水體只好使盡全力逸出氣態水分子，設法讓水面上方的氣態水分子數量重回飽和水分子數量N。但想當然爾，由於蓋子早就打開了，於是水分子數量很少的外界大氣，便會貪婪地一直取走逸出的水分子，所以水面上方空間VA中的水蒸氣分子數量一直無法達到飽和狀態，導致盒子裡的液態水必須不斷地釋出水分子到整個大氣中，直到水乾了，或是…。

是的！或是像圖6.b那樣，整個大氣中，每個體積為VA的空間裡都有N個氣態水分子；如此一來，水面上方VA的空間中的氣態水分子數量，就會保持為飽和水分子數量N個的動態平衡，然後氣態水分子被補捉回水面的速率，等於液態水分子逸出水面的速率，巨觀的蒸發便停止，盒子裡的水量也不會減少了。

然後我們再於每個體積為VA的空間中，補滿數量為M-N的大氣分子，於是大氣壓力便補回1 atm 了！

我這樣說也是有憑有據的，因為體積為VA的空間中，塞入N個溫度為TA的水分子，其壓強換算出來應該是水的飽和蒸氣壓E；然後再在VA的空間中塞入N-M個大氣分子，若令其換算出來的壓強為PA，則 E + PA = 1 atm，因為VA的空間中總共塞入了M個分子，而前面已經定義過了：一個體積為VA空間，充滿了壓強為 1 atm、 溫度為TA的大氣分子，其分子數量應為M。

這真的不是唬爛，而是道爾頓講的：

道爾頓分壓定律：在組分之間不發生化學反應的前提下，理想氣體混合物的壓強等於各組分的分壓之總和。數學描述為：Pt = P1 + P2 + P3 + …，其中 P1 、P2 、 P3、 …為每一個組分的分壓。

所以這到底是什麼意思，意思就是在我們日常生活的一大氣壓下，當溫度為TA時，如果每個體積為VA中的空間都數到N個氣態水分子，那麼我們周邊的大氣中，水分子的含量已然飽和了，於是一杯溫度為TA的水在室外放了再久，它也不會蒸發得越來越少，事實上，它的體積會保持不變，也就是說，我們的絕對溼度飽和了，或是相對溼度達到100%，端看我們愛怎麼講就怎麼講。

那水的飽和蒸氣壓E呢？老實講，解䆁水的微觀蒸發與巨觀蒸發，並不需要用到飽和蒸氣壓E這個概念，因為前面已經說過了，這完全跟水分子補捉/逸出水面的速率達到平衡有關，而水分子補捉/逸出水面的速率又僅受到溫度控制。所以，跟本就不用考量水的蒸氣壓如何影響水分子的蒸發或凝結，那講不出個所以然的。（至少我在網路上找到的說明與討論串是如此…。）

那水的飽和蒸氣壓E到底要幹麻？課本上不都這麼教？這前面也說過了，量壓強P比數分子數量N強多了，既然在指定溫度TA、體積VA的空間中，飽和水分子數量N就等於水的飽和蒸氣壓E，那麼用E去表示N，何樂而不為呢？

另外提一點，就是體積為VA的空間中，溫度為TA的飽和水分子數量N是固定的，亦即飽和蒸氣壓E是固定的，E不受外界壓力影響，只與液體溫度有關（飽和蒸氣壓僅是溫度的函數）。

ps. 見鬼了，以下的中文都是google翻譯的，我只對調了幾個中文用詞的順序與標點而已…。想當初google翻譯出來的結果是不能見人的，難怪古人說士別三日，即更刮目相待。看來google連下圍棋都能連贏六十幾位當代大師，那字母公司下一步要統治世界，恐怕也是指日可待了…。

參見：飽和蒸氣壓（saturation vapor pressure）

1. The vapor pressure of a system, at a given temperature, for which the vapor of a substance is in equilibrium with a plane surface of that substance's pure liquid or solid phase; that is, the vapor pressure of a system that has attained saturation but not supersaturation.

在給定溫度下，「物質的蒸汽」與「該物質的純液體或固相平面」互相平衡（大概是微觀蒸發速率與凝結速率相同的意思吧）時的系統蒸氣壓；即已經達到飽和，但不是過飽和的系統的蒸氣壓。

2. The saturation vapor pressure of any pure substance, with respect to a specified parent phase, is an intrinsic property of that substance, and is a function of temperature alone. For water vapor, the saturation pressure over supercooled liquid differs appreciably from that over ice.

任何相對於指定母相的純物質飽和蒸氣壓，是該物質的固有性質，並且僅僅是溫度的函數。 對於水蒸汽，過冷液體上的飽和壓力，明顯不同於冰上的飽和壓力。

3. Same as equilibrium vapor pressure.

與平衡蒸氣壓相同。

另見：平衡蒸氣壓（saturation vapor pressure）

1. The pressure of a vapor in equilibrium with its condensed phase

與蒸氣冷凝相平衡時的蒸汽壓力

2. This equilibrium is dynamic in that evaporation and condensation are both occurring but are in equilibrium. It is a function of temperature only and is nearly independent of the existence or density of other gases in a system. It may, however, be dependent on the shape of the surface of the condensed phase. More generally, the equilibrium vapor pressure with respect to small droplets containing soluble impurities may be quite different from the saturation vapor pressure.

這種平衡是動態的，因為蒸發和冷凝都發生，但是處於平衡。 它僅僅是溫度的函數，並且幾乎不依賴於系統中其它氣體的存在或密度。 然而，它可以取決於凝聚相的表面的形狀。 更一般地，相對於含有可溶雜質的小液滴，其平衡蒸氣壓力可能與飽和蒸汽壓力完全不同。

會提到這些，是因為在翻找資料的過程中，我發現到維基百科有段對蒸發的特性是這樣寫的：

蒸發的速度取決於多種因素：
物質的溫度：物質的溫度愈高，蒸發愈快。
濕度：空氣的濕度愈高，蒸發愈慢。
氣壓：在氣壓較低或較少的地方，由於施於物質表面的力較小，粒子較容易逃逸，因此蒸發速率較高。
密度：物質的密度愈高，蒸發愈慢。
表面積：物質的表面積愈大，愈多粒子能從物質表面逃逸出去，因此蒸發愈快。
空氣流動速度：由於流動的空氣使流體與蒸發物質之間保持著較大的濃度差距，因此流動速度愈高，蒸發愈快。
蒸發物質中雜質濃度：若蒸發物質中存在其他雜質，蒸發會較慢。
空氣中其他物質的濃度：若空氣中已經充斥著其他已飽和物質，蒸發會較慢。
空氣中是否已有其他物質在蒸發。若空氣中已有一物質在蒸發，另一物質會蒸發得較慢。

首先，先說明一下，這段文字是在分析各項因子對「蒸發速度」的影響，而非「飽和蒸氣壓」。

其次，關於氣壓如何影蒸發速度中，其解釋是低壓施於物質表面（如液態水面）的力小，於以粒子（如液態水分子）容易逃逸（逸出水面，即微觀的蒸發），因此（巨觀的）蒸發速率較高。

如果我對這段敘述的解讀沒錯的話，即氣壓會抑制液態水分子逸出水面，那其概念模型應該如圖7所示。

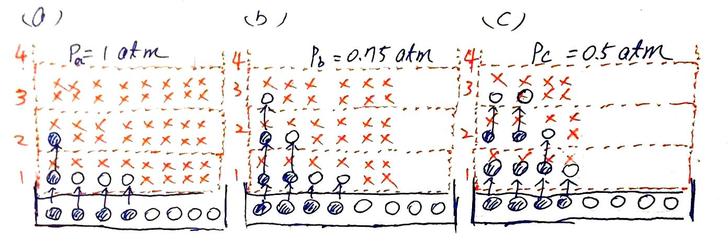
圖7. 若總壓能影響飽和蒸氣壓（分壓）

與圖4.d相較，兩個概念模型都有著水溫Tw、氣溫TA、擁有同樣密閉空間VA的密閉容器，唯一的差別在於圖7的盒子裡裝了N個氣態水分子（數量為圖4.d中的飽和水分子數量N），另其分壓為E（亦即圖4.d中的飽和蒸氣壓E），再加入大氣分子（圖7中的紅色X）使VA中的壓強達到 1 atm，圖4.d的盒子僅裝了壓強為飽和蒸氣壓E的水蒸氣）。

在圖7的概念中，大氣分子會撞擊有意要逸出水面的水分子，這個撞擊減損了水分子的動量，同時便也降低了水分子逸出水面的速率；但由於空間VA中有飽和水分子數量N（即水蒸氣的分壓為飽和蒸氣壓E），所以氣態水分子被水面補捉的速率仍不變。故一進一出的差別下，較小的逸出（微觀蒸發）速率與較大的的補捉（微觀凝結）速率，使得密閉空間VA中的氣態水分子傾向凝結回液面。意思就是，在有大氣分子的情況下，N個氣態水分子早已讓VA中的水分子數量過飽和，而VA中的水分子必須凝結回液態水中，直到VA中的氣態水分子數量減少至N’（壓力與飽和蒸氣壓成反比。

這與前面句「飽和蒸氣壓不受外界壓力影響」矛盾！

所以意思是什麼？意思是，如果飽和蒸氣壓不受外界壓力影響，那麼「蒸發速度受壓力的影響」顯然就不是如維基百科所述，是因為「由於施於物質表面的力較小，粒子較容易逃逸，因此蒸發速率較高」的關係所致。

那為何氣壓越低，蒸發速率會越快？如果飽和蒸氣壓不受外界壓力影響成立的話，那顯然有別的因素在支配著蒸發速率，那會是什麼呢？擴散可能才是主要的原因。

所以，首先，我們先將三杯同樣的水放到沒有水氣、但氣壓不同的大氣中，如圖8.a、圖8b與圖8.c所示（三個外界氣壓分別為 1 atm、0.75 atm 與 0.5 atm，但大氣中都沒有氣態水分子）。

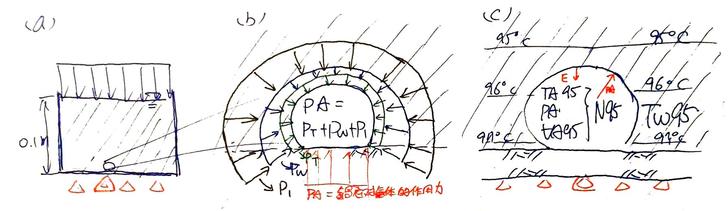
圖8. 總壓不能影響飽和蒸氣壓（分壓）時，總壓對擴散與蒸發速率之影響。

(a) 氣壓為1 atm

(b) 氣壓為0.75 atm

(c) 氣壓為 0.5 atm。水體溫度不變，水面蒸發速率相同，但大氣中體分子數量少（壓強低），氣體擴散散率較大，故水面上的水蒸氣分子越易遠離水面，使水面上方空間內的水蒸氣分子數量M遠低於飽和分子數量N，故微觀的凝結速率減緩，在微觀的蒸發速率不變下，巨觀的蒸發速率變大。

當水杯放下去後，水面即開始蒸發出氣態水分子，而且因外界氣壓不影響飽和蒸氣壓，亦即的液態分子逸出水面的速率也不受外界氣壓所影響。如此一來，圖8中的三杯水，在單位時間中都從水面逸出了相同份量的水分子。這些逸出水面的水分子，起初都會集中在水面附近那層薄薄的空間VA（第1層）中，如此一來，跟上方那層的空間（第2層）相比，第1層中的水分子濃度顯然比第2層高太多了；於是，第1層中的水分子便開始向第2層擴散。

然而，氣態分子的擴散係數與大氣壓力成反比：

擴散係數D…隨氣體…總壓強的下降而加大。

也就是，氣壓越小，擴散係數越大，則氣體越容易擴散。於是第1層中的氣態水分子越容易擴散到上層的空間中，導致臨近水面上方空間中的氣態水分子數量越少，影響即為氣態水分子凝結回水面的速率越慢（因為沒有水分子可以回到水面）。然而，三杯水的水溫是一樣的，亦即液態水分子逸出水面的速率是一致的；所以，凝結的速越慢，水面的巨觀蒸發速率就越快。因此，氣壓越小，水的蒸發越快。

換言之，維基百科寫錯了。

好了，到此為止吧，反正我原本只是想知道飽和蒸氣壓如何決定蒸發、凝結與降雨的。

但該死的，我又看到飽和蒸氣壓等於大氣壓時水就會沸騰…，真是該死的…。

因為在查飽和蒸氣壓的過程，沸騰就像個驅不散的陰魂緊緊地在我耳邊呢喃著：當飽和蒸氣壓等於外界的大氣壓時，水就沸騰了。但我看完了每一篇網路上的文章、與互相攻詰的討論串之後，卻總覺得像霧裡看花似的，那些文字不是含糊地帶過，就是講了一堆表象，卻沒說明任何機制；要不然就是打了一大堆原理，但每個原理兜起來卻又沒個準。

例如水溫未到100度前，蒸氣氣泡裡的氣壓是蒸氣壓，因為比大氣壓小，所以氣泡被壓回去；直到水溫到達100度了，氣泡裡的蒸氣壓等於大氣壓，於是氣泡壓不住，但浮出水面，然後便沸騰了。

可是燒過水的人一定都看過，在尚未沸騰前、水溫未超過攝氏100度時，就已經有些小氣泡出現在鍋底了。重點是，這些小氣泡的體積並沒有明顯的變化，表示其內部壓強等於外部的壓強。那外部壓強有什麼？首先，氣泡與水體的交界面有表面張力，其提供了一點點的圍壓；其次，如果鍋內的水深若有10公分，我們知道10公尺的水深可提供約 1 atm 的壓強，所以水深10公分處的鍋底，又有約 0.01 atm  的水壓。第三，水面上還有 1 atm 的大氣壓。

所以加總起來，氣泡外部的壓強約有 1.01 atm （表面張力提供的壓強太少，先忽略吧），因此，在沸騰前出現在鍋底的氣泡，其內壓至少就有 1.01 atm ，根本不是蒸氣壓（約略超過攝氏100度的水才有1.01 atm），所以外壓要怎樣才能把氣泡壓回去？？更何況，前面說過了，氣泡體積沒變，這只有內壓等於外壓才能發生，在這個條件下，為何又要說內壓是值較小蒸氣壓，然後被外壓是較大的大氣壓回去？

總之，網路上到處都是這類的矛盾…。

所以，沸騰又要怎麼解釋呢？首先，回到剛剛那個例子，在圖9.a中，我們在攝氏25度、氣壓為 1 atm 的大氣中點了一爐火，火上燒了一鍋水，水深10公分，而且已經燒了一段時間了，整鍋水的平均水溫少說也攝氏九十來度，這裡只說「平均」，是因為在燒水的過程中，鍋內各處的水溫度不可能相同的，基本上是上的的水溫最低，底處的水溫最高，高到可能平均下來已然接近攝氏100度。沒錯，依舊是「平均」，因為鍋底的加熱也不可能是完全均勻的，所以某些下面爐火較大的地方，水溫便能達到100度。最後鍋子表面也不是平均的，上面佈滿了大大小小的刮痕，這些地方提供了空間，使吸收了足夠能量的液態水分子能掙脫其他液態水分子間的牽絆，在刮痕處汽化成水蒸氣。然後，今天的第一顆氣泡便冒出來了。

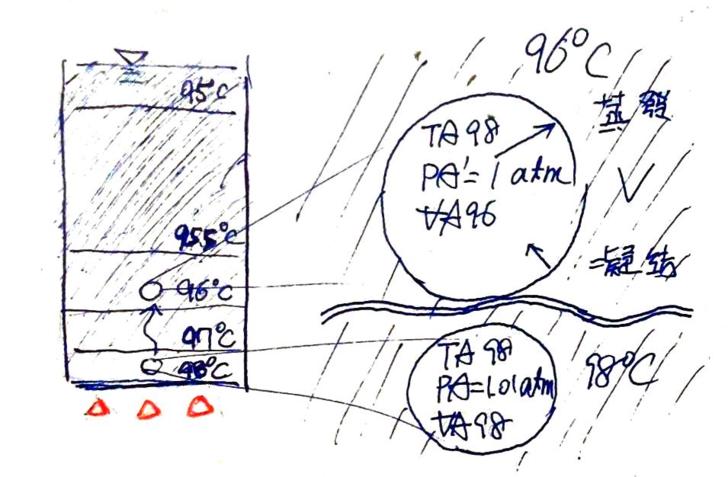
圖9. 燒水時，第一顆氣泡生成！

(a) 鍋底氣泡受力來源

(b) 氣泡放大圖及其圍壓，經力平衡後可知，氣泡內的內壓應為1.01 atm（大氣壓1 atm加上水深0.1 m 時的水壓 0.01 atm）。鍋內水壓變動範圍為1.01 ~ 1 atm（鍋底到水面）

(c) 水汽化後體積快速變大，故氣泡接觸到低水溫區。由於水溫不足攝氏100度，其蒸氣壓小於 1 atm，亦比氣泡的內壓小，於是氣泡內的水分子數量M高過飽和水蒸氣壓N，處於過飽和狀態，使氣泡的內水氣傾向凝結回水中，結果導致氣泡體積減少，乃至於消失。

其次，我們把那顆氣泡周邊的範圍放大，如圖9.b、圖9.c所示，此時便能釐清這顆氣泡的屬性是什麼。在壓力的部份，我們知道，如果我們丟了一團空氣到水裡，若空氣的壓強比周圍的水壓大，這團空氣所形成的氣泡便須到擴大；反之，水壓較大時，氣體體積則會縮小。放大或縮小到什麼程度？直到氣泡內壓強與外界的水壓相同時為止。在一鍋平常的自來水中，這個過程是快速的，快到氣泡才產生，體積便已然停止擴大或縮小、內部壓力與外部的壓力相同。此時氣泡體積不再變化，除非我們將氣泡內的氣態分子移走或加入，此時氣泡體才會變動（縮小或變大），但反應仍是即時的，即氣態分子數量不再改變的瞬間，無泡體積也立刻停止變化。這就像我們在吹泡泡時一樣，在吹泡泡的過程中，我們不斷地把氣態分子吹進泡泡中，於是泡泡便不斷長大；當泡泡封閉離開後，氣態分子不再進入泡泡中，泡泡便不會再變大或縮小了。

講那麼多是因為在燒水的過程中，我們會看到有些氣泡會先出現在鍋底處，並且在那邊停留一段時間。這些氣泡確實會改變體積，但那不可能是在氣泡內部分子數量固定的情況下，氣泡體積調整以平衡內外壓差的速度，因為這種速度太快了；而這些氣泡體積變化的速度，大概就和氣水杯中的氣泡的體積變化速度相似，於是這只有一種可能，那就是氣泡內的氣態分子數量出現變動，而氣泡體積便隨之調整，使氣泡內的壓強維持在與外壓相同的程度。

所以，前述說明了一個重點：在 1 atm、攝氏25度的大氣中煮開水，只要出現在鍋內的氣泡，其氣壓就會與外壓一致。外壓是多少，氣泡的內壓就會是多少，不論煮沸與否都是。

那氣泡的外壓到底是多少？把圖9.a中的那個氣泡放大成圖9.b，首先，氣泡與外界的液態水間有一層交界面，這層界面上的表面張力會提供氣泡內部一份壓強Pt；其次，氣泡在水底，故其上方與周圍的水體亦會提供一份壓強Pw；最後，這杯水放在大氣中，於是水面上的大氣再提供一份壓強P1。各項壓強的值又是多少？首先，表面強力提供的壓強比水壓與氣壓小，所以忽略不計（註1）；其次，氣泡位在水面下0.1公尺處，故其壓強Pw = 0.01 atm（水下10公尺深的壓強約 1 atm），當然，氣泡頂端的水壓較小，下方的水壓最大，但因氣泡小，所以就先都當作氣泡頂端的0.01 atm好了（註1）；最後，大氣壓P1，前面說過了，是 1 atm。因此，氣泡的外壓大約是1.01 atm，於是氣泡的內壓PA也是1.01 atm。（在鍋底處的內壓就是這個定值，不隨水溫而變化；氣泡浮起來時，內壓會再小一點，因為水深減少了，但再少也不會小於 1 atm，因為大氣壓就有 1 atm 了。）

值得一提的是，圖9.b中可看出，作用在氣泡上的大氣壓與水壓，其向下的分力是大於向上的分力（因為一氣泡底部一份是與鍋面相觸），這似乎就是氣泡會被壓在鍋底而不上浮的原因（把一個塑膠製的立方塊小積木放到臉盆裡，直接壓到臉盆底部的平面上，一定要彼此貼合，用力壓緊，把兩面表面間的水趕走。放手猦小積木不會浮起來，因為積木下方沒有水壓，以供向上的浮力，於是積木只會被頂端那面的向下水壓壓住，貼在臉盆底部上不來。）

那其他的參數呢？圖9.c中可看出，雖然這顆氣泡是在鍋底一個小刮㾗處發生的，且該處的局部水溫可能達到了攝氏100度。但一水撮液態水變成氣態後，其體積會膨脹不少，於是這膨脹的大氣泡會遠遠大於原本鍋底處的局部高溫範圍，繼而使自已環繞在周邊較低的水溫中。

我們知道燒水時，鍋內的水溫是向鍋頂遞減的，於是較低的水溫Tw95多少呢，就先說是攝氏95度吧。此時，氣泡的體積可量測，為VA95；溫度來自汽化的液態水，應該要是攝氏100度，但我們先說這氣泡在鍋底待了一兒，於是溫度降到與周邊的水溫一致好了（註1），那就是T95（攝氏95度）；再來，外界的水溫已知，為Tw95（攝氏95度），因此可知攝氏95度時的水蒸氣壓是E95。因此根據理想氣體方程式P V = N R T可知，在體積為VA95的空間中，達到巨觀蒸發停止時的飽和水氣分子數量應為：

N95 = (E95 VA95) / (R Tw95)，…………(1)

為已知值。這是什麼意思？意思是，如果氣泡中的水蒸氣分子數量比N95多（或可說氣泡中的壓強大於攝氏95度時的水蒸氣壓），則氣泡中的水蒸氣分子處於過飽和狀態，微觀的凝結速率大於蒸發速率，因此巨觀的蒸發速率是負值，即水蒸氣會凝結回氣泡外的水體中；反之，若氣泡中的水蒸氣分子數量小於N95，氣泡中的水蒸氣處於未飽和狀態，水體會蒸發到氣泡中；若兩者相等，氣泡中的水蒸氣剛好飽和，巨觀的蒸發停止。

因此，關鍵在於氣泡內的空間VA95中，到底裝了多少個氣態水分子M95？先前假設好了，氣泡內氣體的溫度是TA95（等於Tw95，前面假設的），壓強PA是1.01 atm，而重點是，氣泡內的氣體分子全是由水汽化而來的，也就是說，全都是氣態的水分子！於是我們又可以透過 P V = N R T進行計算，可知氣泡內的氣態水分子數量應為：

M95 = (PA VA95) / (R Tw95)。…………(2)

式1與式2可看出，VA95、T295與R是一樣的，於是氣泡內飽和水分子數量便僅由E95決定，而氣泡內的氣態水分子數量則僅由PA決定。水溫為攝氏95度時的飽和蒸氣壓E95經查表為0.8342 atm，PA則為1.01 atm，故知氣泡內的氣態水分子數量M95大於飽和水分子數量N95，即氣泡分的氣態水分子處於過飽和的態中（註2），所以水蒸氣會凝結回水面，結果就是就是我們的第一顆氣泡體積會減小。但不管如何減小，氣泡內的水分子數量仍舊會超過飽和水分子數量，於是氣泡只好不斷減少，直到消失為止。

事實上，如果仔細觀察燒開水的過程，確實可看最初出現在鍋底的氣泡會發生這種情形。不過通常大火燒水時，爐火加熱的能力，比單一顆氣泡中蒸發/凝結時的能量交換大上太多個數量級，因此鍋底只要出現氣泡，便是一個接一個地冒上來、浮出水面，看不見氣泡消失的現象。此時只要把火關掉，或是將瓦斯關到最小（爐火只剩中間那圈），這時候水溫便會慢慢冷卻下來，方才還在劇烈冒泡的地方，速度也減緩了，直到有些氣泡停留在鍋底，然後，碰！消失！（註3）

（註1：忽略表面張力提供的壓強，又使用氣泡頂端較小的水壓來代替全部的水壓，只會低估氣泡的內壓PA，故實際上，氣泡內的水分子數量應該比未忽略時更多，故氣泡內的氣態水分子更容易凝結回水面。另若不假設氣泡中的溫度TA降溫至周邊的水溫Tw，則氣泡中的氣態水分子的溫度應較Tw更高，較高的溫度使氣態水分子具有較大的速度，增加撞擊而凝結回水面的速率。）

（註2：由於氣泡中的水蒸氣壓強一直為1.01 atm，而整體水溫被加熱到沸騰溫度前〔比攝氏100度高一點點，就先當作是攝氏100度吧〕，其飽和蒸氣壓都不會超過1.01 atm，於是在沸騰前的每一個氣泡中其水蒸氣分子數量都處於過飽和狀態，因此巨觀來看，氣泡中的水蒸氣在沸騰前是不斷凝結回水中的。

（註3：也許有人仔細觀察過燒水的過程，然後他們會說：「不！剛冒出的泡泡不會消失！」不要擔心，我也遇過這種事，但此事先放著，最後再解釋。）

前情提要：我們的第一顆氣泡消失了。

不過，幸好，我們的爐底還在持續加熱。

圖10. 持續加熱對氣泡內部微觀蒸發與微觀凝結速率之影響

(a) 氣泡底部之鍋體升溫較快，連帶加周邊鍋體，使氣泡底部周邊的水溫上升，並向氣泡內提供蒸氣，以維持氣泡體積。同時，熱能由氣泡底部經過蒸發進入氣泡，再由上方的凝結回到水體中，有助於熱量傳遞到上層低溫水體，使水溫上升。

(b) 鍋底高溫水層厚度持續增加，更多的水蒸氣進入氣泡，使氣泡體積增加。

於是，鍋底附近的水溫Tw97被加熱到攝氏97度了（圖10.a），新形成的氣泡中，飽和水分子數量的上限抬升到比N95更大的N97，飽和上限更接近氣泡內的水蒸氣分子數量，於是凝結便減緩了。此時，我們可以看見氣泡在鍋底停留得更久，久到因為氣泡底部的鍋子沒與水接觸，而比周遭與水接處的鍋體升到更高度溫度，這樣的溫度讓氣泡底部外圍小部份的水溫升高，升高到飽和蒸氣壓E100與氣泡內的壓強PA相同，亦即該處的水溫使飽和水氣分子數量上限N100提升到與氣泡內的分子數量M100相同，此時氣泡底部周邊的水體便可以向氣泡內供應水氣分子了；當然，在氣部上半部水溫所處的飽和蒸氣壓E97仍低於氣泡內的壓強PA，故氣泡內的水蒸氣分子則仍在向水體中凝結。如果底部蒸發的速度等同於上部凝結的速度，那這個氣泡便會維持同樣的大小，而不會消失了。

而這也是我們在燒水的過程中，看到有些小氣泡停留在鍋底處，不變大也不變小的原因。

此外，由於蒸發是液態水的能量被帶離水體（蒸發時水溫降低），反過來說，凝結便是將能量由蒸氣中帶回水體。因此鍋底處的熱能傳遞路線除了經由水體的對流與傳導外，透過氣泡中的蒸發與凝結似乎也是另一種路徑，即如圖10.a中所揭示的，氣泡下緣周邊的水，當其溫度高到使飽和蒸氣壓超過氣泡內壓時，便可透過蒸發而將熱能帶進氣泡中；然而氣泡上方的水體因溫度較低，使其飽和蒸氣壓比氣泡的內壓小，於是氣泡的蒸氣便凝結回到氣泡上方的低溫水體中，連帶將熱能帶過去，進而加熱氣泡上方的低溫水體。也就是說，爐火燒水的熱能在氣泡中轉了一圈又回到水中，導至爐火的供熱，應該有大部份仍是用於加熱水體之用上，更別提還有對流所造成的熱量傳遞作用。

於是，連同水體的對流、傳導作用，鍋底附近的水溫Tw98現在被加熱到攝氏98度了（圖10.b）。

此時，這個氣泡已經在鍋底停留了一段時間，其下方與水蒸氣相觸的鍋體持續升溫，並連帶提升了周邊鍋體的溫度，然後加熱氣泡底部周遭的水體溫度。此時這些熱量一直透過蒸發而移入氣泡裡，但顯然爐火提供熱量的速度快得多。所以在僅有氣泡面蒸發的條件下，爐火提供的能量應該有辦法蓄積在氣泡底部周遭的水體中，讓小區域中的水溫略為超過沸騰溫度（令為攝氏100度），例如攝氏100.2度。此時氣泡底部的蒸發速度增加，氣泡上方周邊的水溫則因增加到攝氏98度，而令氣泡上方的凝結速率持續減少（E98比E97更接近氣泡內壓PA）。於是當氣泡下的的蒸發速率大於上方的凝結速率時，氣泡的體積便增加了。

氣泡的體積增加，浮力便上升，加上水是非線性系統，隨便一個小小的水流便能放大成渦漩，更何況鍋底還在加熱，不斷提供水流向上對流的動力。於是乎，某個渦漩掃過鍋底，然後有一顆氣泡脫離了鍋底的束縛，向上升起。

圖11. 第一顆浮起的氣泡，及上升路徑周邊水溫之遞減與其影響

這第一個浮起的氣泡，命運也可說是乖舛，因為它生成的環境是在鍋底的高溫區，若依前面的假設，其生成時的溫度TA應為攝氏98度（實際上應該要有攝氏100度，因為畢竟是由高溫水汽化而來的，但就先這麼用吧），體積可量測，故令為V98，內壓則說過了，永遠是外壓PA（1.01 atm）。但在燒水的過程中，鍋子上方的水體，因其遠離爐火、僅能靠對流增溫，故鍋子上方的水溫必然較鍋底處的水溫低，因此我們就先假設鍋子上方的水溫（Tw96）是較低的攝氏96度吧（如圖11所示）。

於是，當這顆氣泡進入較低溫的水層時會發生什麼事？

首先，氣泡的內壓與外壓相同，大氣壓 1 atm 是不變的，而氣泡在水中的深度卻變小了，在鍋底處是 0.01 atm（水深 0.1 m），往上浮的過程中會逐漸降低到 0 atm（水深 0m）。根據

P V = N R T

可知，氣泡內的水分子數量若不變，則當氣泡內的強降水減少而降低時，其氣泡的體積可能會增加，或是溫度也可能會降低（不過基本上我直覺是前者）；也有可能氣泡在上升過程中，因遭遇到鍋內上層降低溫的水體而降溫。但不論體積或溫度的變化為何，可以確定的一點是，不論氣泡在0.1 m 水深中的何處，其內壓一定是在 1.01 atm與1 atm間變動（鍋底的大氣壓加深 0.1m 水壓，與水面的大氣壓）。

換言之，完全由水蒸氣所構成的氣泡，其內壓不外乎就是1.01 atm與1 atm，但鍋內的水溫由下往上遞減，使氣泡所接處的水溫不斷減少，有多少？一定比鍋底最下層的溫度小（例如圖11中的氣泡，處於攝氏96度的水體中）。低於攝氏100度的水體，例如圖11的水溫T96為攝氏96度，其飽和蒸氣壓E96必然小於 1 atm ，意味著在某一個體積的空間中（圖11中的VA96，由原本在鍋底時的VA98擴大而來）中的飽水分子數量N96，必然小於同樣體積VA96中、溫度為TA96（TA96≒Tw96，要≒TA98也是沒關係的，反正氣泡上浮後，水蒸氣分子的數量只會少，不會多）、壓強為1 atm 的氣體分子數量 M96，即氣泡內的水分子數量處於過飽和狀態，微觀的凝結速率大於蒸發速率；而且越往上走、水溫越低，這個速率差異還會越大。於是，我們第一個上升的氣泡，體積會越來越小，最後，碰！消失了。（其實原理就和前面第一個出現的氣泡一樣）

因此，當燒水時，剛開始有氣泡往上浮時，這些氣泡通常是無法到達水面的（註4）。

（註4：若火開得太大，氣泡越上浮體積越少的現象可能不好觀察，但可以把火關小，自然就能看到氣泡在上浮的過程中消失了。然後，隨著鍋底的冷卻，氣泡出現的速率越來越少，直到僅停留上鍋底上而不上浮，最後，這些氣泡也會消失不見。）

當然，氣泡雖然消失了，但我覺得它終究還是有貢獻的，畢竟，在燒水的過程中，僅能靠對流作用將鍋底的熱能向上方傳送。然而，當水蒸氣氣泡開始脫離鍋底向上飄浮後，連帶著將周遭的高溫水流一起向上方帶，加速了鍋底熱能往上傳送的速度。

於是，越多的氣泡向上浮（雖然多數在到達水面前便壯烈成仁……凝結回水中了），使得鍋底上、下的溫差快速減少，整體的水溫越來越多，氣泡內部的水蒸氣在上升時越不易凝結回水體， 故終將有第一顆氣泡自水面冒出頭，然後是第二顆、第三顆、第千千萬萬顆。這些快速產生又浮水面的氣泡，使水流擾動的範圍達到整個水體，於是水溫分佈被攪得比早前更均勻。最後，整鍋水的水溫便能在短時間達到攝氏100度。

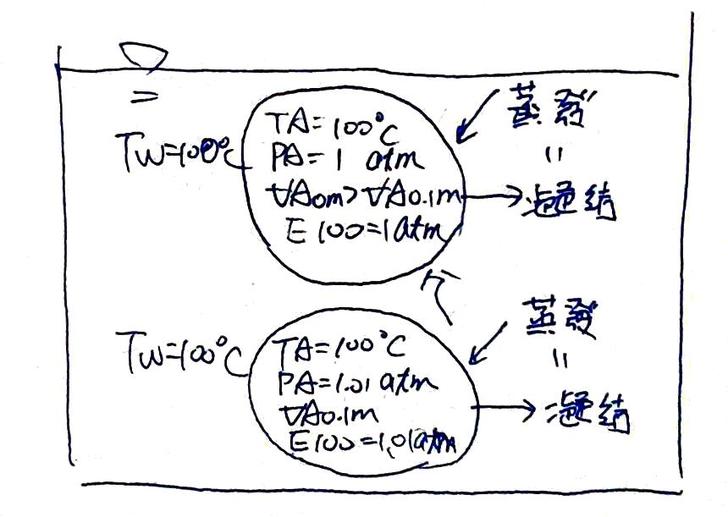
圖12. 完全沸騰

當整鍋水都均勻地達到攝氏100度後（如圖12），整鍋水各部份水體的飽和蒸氣壓都達到 1 atm，可知若溫度為攝氏100度的水蒸氣在水體中佔據了一處體積為VA的空間，其飽和水分子數量應為N100。然而蒸氣氣泡裡的內壓也是 1 atm，故實際存在於氣泡內的分子數量M100會等於飽和水分子數量N100，亦即此時氣泡內水分子的微觀蒸發與凝結速率相等，所以巨觀的水分子凝結停止。故水體中任一處出現一顆氣泡，這顆氣泡便不會再消失，只會毫無保留、義無反顧地衝出水面，於是，水就沸騰了。

而這也是我們說「當飽和蒸氣壓等於大氣壓時，水會沸騰」的原理。

最後，總結一下：

1. 飽和蒸氣壓E僅與溫度T有關，在意義上更像個標誌，標示著在指定體積為V的空間中的飽和水分子數量N。

2. 體積為V的空間中，可塞入任意個溫度為T的水蒸氣分子；但若塞入水蒸氣分子數量M超過飽和水分子數量N，則氣態水分子傾向凝結成液態；數量M不足N，則液態水分子傾向蒸發成氣態；M與N相同，則蒸發與凝結達到動態平衡。

3. 在已知溫度T與體積V的空間中，M個水蒸氣分子可求其形成之壓強P。在已知溫度T與體積V的空間中，飽和水分子數量N亦可換算成壓強，定義為在溫度T時的飽和蒸壓E。

4. 由上述故可知，在已知溫度T與體積V的空間中，若僅有水蒸氣分子，其構築的壓強P>E ，水蒸氣分子處於過飽和狀態，氣態水分子傾向凝結成液態；P

5. 水沸騰前（飽和蒸氣壓 ≡ 1atm），在水中產生的氣泡完全由水蒸氣組成，不限位置與溫度，其壓強必為外壓，量值為大氣壓加水壓。且因為尚未沸騰，水體中多數位置的飽和蒸氣壓皆小於 1 atm，

6. 水沸騰前（飽和蒸氣壓 ≡ 1 atm），氣泡除了在非常接近鍋底的水體外，其他位置的飽和蒸氣壓E都小於 1 atm ，亦小於氣泡的內壓P，因此氣泡中的水蒸氣分子數量M皆大於飽和水分子數量N，故氣泡中的氣態水蒸氣傾向凝結回液態水，使氣泡變小，即便是已在上升的氣泡仍是如此。

7. 氣泡的存在有助於熱量由水的底部往上方傳遞，若氣泡浮起，其帶動的水流更可將可觀的熱量帶至水面，使整體水溫之分佈更平均。

8. 當整體水溫達到飽和蒸氣壓E為 1atm（約攝氏100度），飽和蒸氣壓E與氣泡內的壓強P相同，意味著氣泡內的氣態水分子數量M等於飽和水分子數量N，於是蒸發與凝結速率達到動態平衡，氣泡便不再變小，除了可直接上浮至水面，其體積亦因壓力降低（上浮後水深減少，故水壓降低）而變大。

9. 於是水就沸騰了。

為了證明上述的想法是正確的，我還特定為此去燒了一鍋水，結果，該死的，怎麼不是我想像中的那個樣子！！真的，相信我，有空的人自己也去煮一鍋水，就會發現早在水溫上升到九十幾度前，鍋底便出現了許多小小的氣泡，約末這個句點「○」那麼大。我沒有工具可以量溫度，但我相信此時的溫度僅有攝氏八、九十度出頭，因為大量上浮的氣泡還要很久之後才會出現。而且更糟的是，這些氣泡不會消失，還越來越多，遍佈整個鍋底，然後開始合併成大氣泡，然後開始上浮，然後從來沒有消失！一個也沒有！即便關掉火也是，氣泡只是停止出現，但即便等了很久，水溫降下來後也不會消失！為此我還把這鍋水泡到更大的桶子裡，結果還是一樣！

這個問題消耗了我整個晚上的時間，還有一大堆瓦斯，然後當某一刻，我將這鍋終於煮沸的水冷卻再加熱後，突然發現剛才那些小氣泡不見了！

所以，原來是有什麼東西在水裡，加熱後跑出來變成氣泡，整鍋水沸騰後跟著大量的氣泡一同逸到空氣中。待水冷卻後，那東西早已消失了，於是重新加熱後，便不會再出現這些意料之外的氣泡！

所以，那東西會是什麼，我想，最有可能是消毒用的氯氣了。於是我上網查了一下：

自來水在淨水場加氯氯消毒過程中，水中有機物和氯反應會形成三鹵甲烷，其主要生成物包括氯仿（註：即三氯甲烷）、一溴二氯甲烷、二溴一氯甲烷、溴仿等四者合稱三鹵甲烷。——高雄市政府環境保護局

又：

（本研究）全面檢測各縣市自來水之消毒副產物三鹵甲烷…，三鹵甲烷組成份以三氯甲烷濃度佔57.5 ％最高，三溴甲烷5.0 ％最低。——自來水三鹵甲烷含量之調查研究

三氯甲烷就是氯仿，氯仿的沸點為攝氏61.15度，即在攝氏61.15度時，氯仿的飽和蒸氣壓為1 atm ！

所以在燒水時，水溫一但超過攝氏61.15度後，水中含有的氯仿便會開始汽化成氣態，且因鍋底處的水溫最高，故氯仿氣泡便是由鍋底處開始出現的。然而水中的氯仿含量不高，於是無法快速形成更大的氣泡，而因體積有限，氣泡便無法上浮，故只會停留在溫度逐漸升高的鍋底處。

此時，氯仿氣泡內的壓強P為1 atm，但由於水溫T早已超過攝氏61.15度，因此，怎氯仿的飽和蒸氣壓E便會超過 1 atm，意即氣泡內的氯仿分子數量M低於飽和分子數量N，所以水中的氯仿會持續地蒸發到氣泡中！所以氣泡不會消失！所以還會慢慢長大！而當氣泡大到終於可以浮起時，整鍋水的水溫早已超過攝氏61.15度，因此氣泡在上升的過程中，也不會將氯仿凝結回水中，因此氣泡便能上升到上面上了！最後，由於氯仿氣泡出現時，水溫已然超過攝氏61.15度，因此即便此刻將爐火關掉，但氣泡周邊的水溫仍要一段時間才能降低，於是，氣泡便會一直杵在鍋底不肯消失！

結論：這些最早出現的氣泡不是水蒸氣，而是氯仿蒸氣（連同其他一堆三鹵甲烷的分子），它們不是純水沸騰過程中該出現的東西！

幸好我們可以移除它們，先把水燒開了，讓這些雜質逸出，然後再降溫重燒一次，這回就看到水沸騰的真正過程了。

還有，阿門，這回沸騰現象就和我當初想像中的一模一樣了。

最後，突沸就簡單了。當裝水的杯子光滑無瑕疵（如玻璃杯），杯中的水沒有雜質，連多餘的擾動也沒有。此時，水中沒有汽化核，氣泡無法出現，於是熱源供給到水中的能量，便只能透過傳導與水面蒸發這兩種路徑，將熱量由杯子向外界傳遞。所以供熱功率很容易超過水體的散熱功率，故水體便可被加熱超過攝氏100度。此時，只要在過熱的水中加入一些汽化核，如咖啡粉、湯匙等雜質，甚至只是攪動時帶進的氣泡，水蒸氣氣泡便會依附著這些汽化核產生。

然而，因水溫早已起過攝氏100度，即氣泡中的飽和蒸氣壓E超過 1 atm。但氣泡內的壓強僅等於外壓的 1 atm，表示著氣泡內的水蒸氣分子數量M低於飽和分子數量N，故水體會快速地將水分子蒸發到氣泡中，令每個氣泡快速地增大體積。由於一次加入了很多的汽化核，每個汽化核會產生很多氣泡，每個氣泡又快速加大體積，於是杯內突然出現大量上升的氣泡，連同沸水一同衝出杯口，突沸便發生了。