在牛頓的時代，物理學者對於遠距離施力感到難以理解，但終牛頓一生也沒有想通。到了19世紀，重力場理論興起，這個疑惑終於得到舒解。

場這個觀念是19世紀法拉第在研究電磁現象時所提出的，指的是遍佈整個宇宙在每一個點都有值的物理量。這個量可以是純量、向量、或張量。場是一個物理學中劃時代的觀念，與力、能量、四維空間可以相提並論的創見。從此以後，場成為理解物理不可或缺的觀念。現代物理學中的相對論、電磁學、與量子場論全都建立在場的觀念之上。

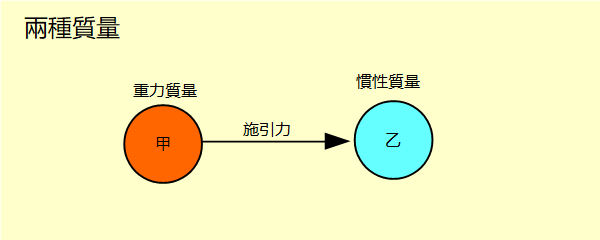
在重力定律中有兩個粒子的質量。一個粒子施力，另一個粒子受力。施力的粒子質量稱為重力質量，受力的粒子質量稱為慣性質量。也就是說，質量有兩種。讓施力的粒子為甲，受力的粒子為乙。甲的質量是重力質量；乙的質量是慣性質量。依照第三運動定律，乙也會施相等方向相反的重力於甲。在這種情況下，乙的質量是重力質量，甲的質量是慣性質量。無論任何粒子，慣性質量與重力質量的值相等而功能不同。這就產生一個問題，這兩種質量的本源是否相同？關於質量來源，後續到量子論再討論。

從重力定律推衍重力場極為簡單，只要剔除其中受力的粒子，只留下施力的粒子。由這個粒子所產生的重力場，在空間任意一點的值是
  重力場值 = 重力常數 × 粒子的質量 ÷ 點與粒子的距離²
這個值是向量。方向是點至粒子的方向

重力場的量綱與加速度相同，所以重力場並不是力場，而是加速場，應該稱為重力加速場。物體受到重力加速場的作用會加速，而加速度與物體的質量無關，只與所在位置的重力場值有關。也就是說，粒子與所在位置的重力加速場作用，而不是隔空與其他粒子作用。一個粒子的位置可以有其他粒子的重力加速場。從重力加速場的公式可以得出，施力粒子本身的位置有本身的重力加速場值是0。

重力加速場的觀念提供一個新的思路來看重力。

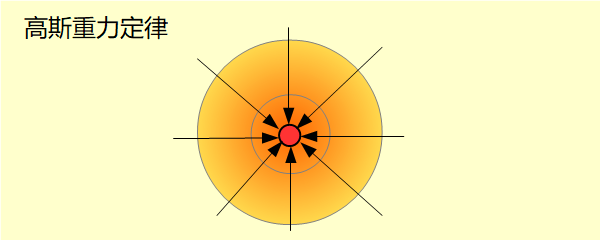
與一個粒子相等距離的空間點形成一個正圓球。這個正圓球面上每一個點的重力加速場的絕對值都相等，方向都與球面垂直指向粒子。因為指向球內所以取負值。正圓球面的重力加速場向量和是0。所有的重力加速場絕對值的和是
  -4π×重力常數×粒子質量
。這個值代表重力加速場於球面的重力通量，是通過球面的重力加速場的總量。這個公式顯示重力場的球面通量與球的大小無關。

重力加速場的重力通量並不限於球面。任何三維形狀的表面都可以計算通量。計算的方法是取重力場垂直表面的分量的值。如果向外取正值，向內取負值。所有值的和就是這個表面的通量。任何包含粒子的形狀表面的通量都相等。這是高斯重力定律。

高斯重力定律證明當同等的重力通量通過不同距離的球面，球面每一點的加速度是通量除以球面積。由於球面積是與球心的距離平方成正比，高斯重力定律完美的解釋為什麼重力加速度與距離的平方成反比。

重力加速場可以算做一種新的結構模式。物體有結構。汽車有底盤、引擎、輪胎等部件所構成。房子由地基、牆壁、屋頂等部件所構成。同樣的，物理模式也可以有結構。重力模式的結構就是兩個粒子的質量、距離、及重力常數所代表的機制。重力加速場改變了原本的重力模式的結構。重力改由重力加速場與受力粒子所組成。重力加速場不再侷限於受力的粒子而擴及全部空間。這就說明相同的外部模式可以有不同的結構模式，就像外觀相同的汽車內部結構可以不同。

與重力定律相比，重力加速場定律其實只是將受力粒子的質量從重力定律的公式中剔除而已。公式上的些微改變實際上代表著觀念上的重大變革。牛頓的重力只有當有受力的粒子才存在於受力點。粒子是離散的 ，數量是有限的。重力加速場不同。重力加速場遍佈所有的空間點，是連續的，是全面的。重力加速場的值在沒有受力的粒子時是無法觀察的。這就造成一個疑惑，沒有受力的粒子時還有重力加速場麼？重力加速場是真實存在的，還只是一個想像的觀念？如果認為重力加速場無論有沒有受力粒子仍然存在。那麼沒有受力粒子如何證明重力加速場的存在？

從重力加速場的觀念與公式衍生出許多疑問：是每一個粒子各有一個重力加速場，還是共有一個重力加速場？當沒有粒子時，還有沒有重力加速場？粒子如何產生重力加速場，產生的場為什麼與質量成正比？重力加速場與粒子作用時，如何隨著粒子的質量調整重力？在粒子移動時重力加速場如何與粒子同步移動？

除了以上的疑問外，還有一個更重要的問題。無論重力定律或重力場都是三維空間，而空間是四維。四維空間的重力應該如何理解？