2006年美國高中生數學競賽最難題目(1695位參賽者,只有3位參賽者答對)
有A,B,C,D,E 共五台電腦,想利用丟銅板的方式決定任兩台電腦間是否要連線,
如果出現正面,則連線,如果出現反面,則否。
每個傳到其中一台電腦的訊息將會同時傳到其他和這台有連線的電腦。
試求每一台電腦都能從其他所有電腦收到訊息的機率。
請把想法和過程寫下。
我們稱可以達到題目要求的情況為"完全連線",反之稱為"不完全連線"。
5個電腦以5個點ABCDE表示
5個電腦的連線情形可以用5邊形+對角線表示
∴可以有10條連線
∵每條線有連線未連線之分
10
∴有2 =1024種可能的情況
每個情況出現機率相同
把所有的情況分為有0、1、2、3、4、5、6、7、8、9、10個連線的圖形
∵任一部電腦要得到其他4部電腦的資料,至少必須有4條連線
∴有0、1、2、3連線的圖形是"不完全連線"。
∵如果光4台電腦連線,最多是6條連線
也就是說 有7、8、9、10條連線的情形
必定可以得到第5部電腦的資料。這些情況都算"完全連線"。
剩下來的就是計算圖形中有4、5、6條連線中"不完全連線"的情形
(1)6條連線的情況中,"不完全連線"的情形,總共有5種,圖形例子是4邊形ABCD+對角線2條。
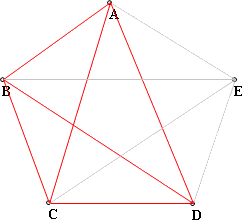
也就是說,只在5邊形的圖形中數數看頂點在ABCDE的的4邊形個數即可。
(2)5條連線的情況中,"不完全連線"的情形,總共有30種,圖形例子是"4邊形+對角線"少一個邊。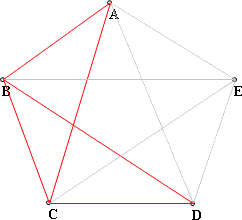
所以有5╳C(6,1)=30種
(3)4條連線的情況中,"不完全連線"的情形比較複雜,有兩種狀況:
第1種例子是"4邊形+對角線"少2個邊。
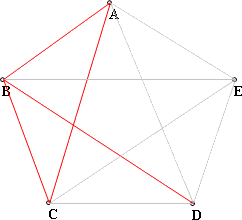
共有5╳C(6,2)=75
第2種例子是三角形ABC+DE。也就是說,只在5邊形的圖形中數數看頂點在ABCDE的的3角形個數即可。
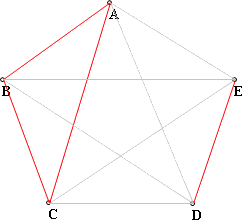
故共有C(5,3)=10種
所以"不完全連線"的狀況總共有
01 2 3 4 5 6
1+10+C(10,2)+C(10,3)+(75+10)+30+5 =296
=1+10+45+120+85+30+5
故可以"完全連線"的機率是
(1024-296)/1024=91/128


 字體:小 中 大
字體:小 中 大












