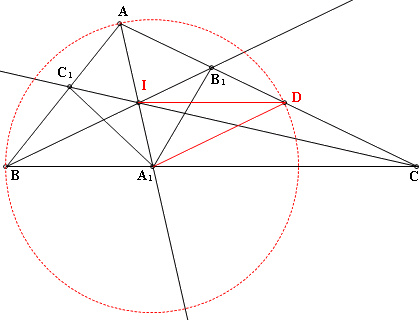
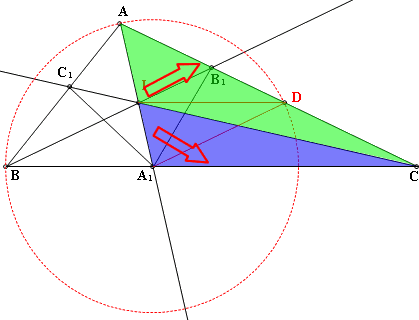
6.在三角形ABC內，∠A=2∠B=4∠C ，角A、角B及角C的內角平分線，分別交對邊於點A1、B1及C1。試證A1B1=A1C1。

方法２：轉換線段比

（１）作輔助線

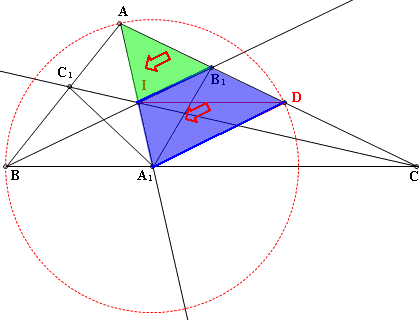
（２）證明全等

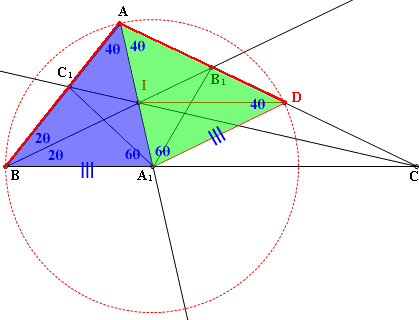
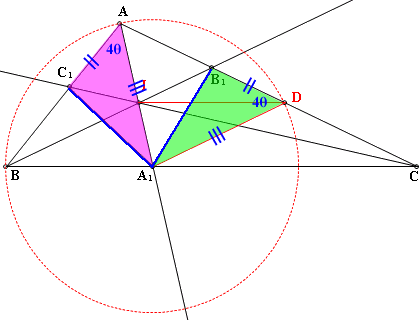
在△Ａ₁ＡＢ和△Ａ₁ＡＤ中
∵Ａ₁Ａ＝Ａ₁Ｄ
∴∠Ａ₁ＤＡ＝∠Ａ₁ＡＤ＝４θ

∵∠Ａ₁ＢＡ＝∠Ａ₁ＤＡ＝４θ＝∠Ａ₁ＡＢ＝∠Ａ₁ＡＤ
且Ａ₁Ａ＝Ａ₁Ａ（共用）
∴△Ａ₁ＡＢ≡△Ａ₁ＡＤ（ＡＡＳ）
得ＡＢ＝ＡＤ

（３）證明平行

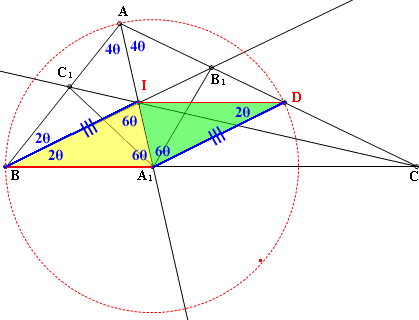
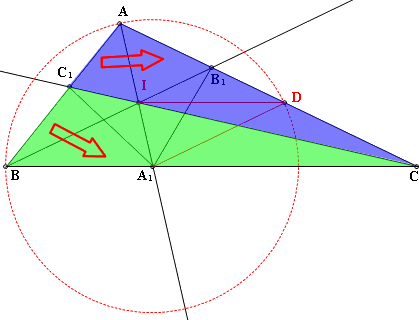
（４）ＡＢ₁：Ｂ₁Ｄ＝ＡＩ：ＩＡ₁

（５）ＡＩ：ＩＡ₁＝ＣＡ：ＣＡ₁

（６）ＢＣ₁：Ｃ₁Ａ＝ＢＣ：ＣＡ

又△ＡＢＣ～和△ＡＡ₁Ｃ（ＡＡ相似）

故ＢＣ：Ｃ＝ＡＣＡ：ＣＡ₁

也就是ＢＣ₁：Ｃ₁Ａ＝ＡＢ₁：Ｂ₁Ｄ

又ＡＢ＝ＡＤ，∴Ｃ₁Ａ＝Ｂ₁Ｄ