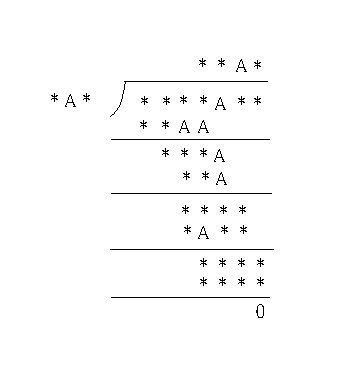
由第一區的除式：（□ＡＢ╳Ｃ＝□□ＡＡ）
和第二區的除式：（□ＡＢ╳Ｄ＝　□□Ａ）
合併判斷得知兩個乘數不同，但個位數相同
可以推知Ｂ＝１～９的乘數中，個位數會出現兩次以上

對照下表：

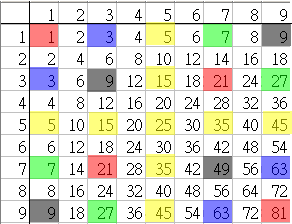
可以推得，Ｂ可能＝２，４，５，６，８或０

設Ａ＝１由第三區的除式來判斷：（□１□╳１≠□１□□）顯然無解
設Ａ＝０由第一區的除式來判斷：（□０Ｂ╳□＝□□００）
可以推得Ｂ＝０，但題目規定Ｂ≠Ａ　　所以Ａ≠０或１

∵Ｂ≠Ａ　可以推知

當Ｂ＝２時　Ａ可能＝４，６，８。
由第一區的式子來檢驗：（□ＡＢ╳Ｃ＝□□ＡＡ）
　□４２╳２＝□□８４　　　　□４２╳７＝□□９４
　□６２╳３＝□□８６　　　　□６２╳８＝□□９６
　□８２╳４＝□□２８　　　　□８２╳９＝□□３８　無解

當Ｂ＝４時　Ａ可能＝２，６，８。
由第一區的式子來檢驗：（□ＡＢ╳Ｃ＝□□ＡＡ）
　□６４╳４＝□□５６　　　　□６４╳９＝□□７６
　□２４╳３＝□□７２　　　　□２４╳８＝□□９２
　□８４╳２＝□□６８　　　　□８４╳７＝□□８８（Ｏ）

當Ｂ＝５時　Ａ可能＝３，７，９。
由第一區的式子來檢驗：（□ＡＢ╳Ｃ＝□□ＡＡ）
但Ｂ＝５時，個位數只可能是０或５　明顯不合。

當Ｂ＝６時　Ａ可能＝２，４，８。
由第一區的式子來檢驗：（□ＡＢ╳Ｃ＝□□ＡＡ）
　□２６╳２＝□□５２　　　　□２６╳７＝□□８２
　□８６╳３＝□□５８　　　　□８６╳８＝□□８８（Ｏ）
　□４６╳４＝□□８４　　　　□４６╳９＝□□１４

當Ｂ＝８時　Ａ可能＝２，４，６。
由第一區的式子來檢驗：（□ＡＢ╳Ｃ＝□□ＡＡ）
　□２８╳４＝□□１２　　　　□２８╳９＝□□５２
　□６８╳２＝□□３６　　　　□６８╳７＝□□７６
　□４８╳３＝□□４４（Ｏ）　□４８╳８＝□□８４
∴除數有三種可能
　□８４╳７＝□□８８
　□８６╳８＝□□８８
　□４８╳３＝□□４４

(１)□８４╳７＝□□８８
由第二區的除式來判斷：（□８４╳□＝□□８）
∵□８４╳２＝□６８　可能有
　１８４╳２＝３６８　２８４╳２＝５６８　
　３８４╳２＝７６８　４８４╳２＝９６８　四種
由第三區的除式來判斷：（□８□╳８＝□８□□）
∵１８４╳８＝１４７２　２８４╳８＝２２７２　
　３８４╳８＝３０７２　４８４╳８＝３８７２（Ｏ）
所以推的　除數可以是４８４

把剛剛所得結果填入來推理。
∵４８４╳７２８□＝□□□□８□□
　４８４╳７２８３＝３５２４９７２
　４８４╳７２８４＝３５２５４５６
　４８４╳７２８５＝３５２５９４０
　４８４╳７２８６＝３５２６４２４
　４８４╳７２８７＝３５２６９０８
　４８４╳７２８８＝３５２７３９２
　４８４╳７２８９＝３５２７８７６（Ｏ）

　　　　　　　７２８９
　　　－－－－－－－－－
４８４）３５２７８７６
　　　　３３８８　　　
　　　　－－－－－－－－
　　　　　１３９８
　　　　　　９６８
　　　　－－－－－－－－
　　　　　　４３０７
　　　　　　３８７２　　
　　　　－－－－－－－－
　　　　　　　４３５６
　　　　　　　４３５６
　　　　－－－－－－－－
　　　　　　　　　　０
(２)□８６╳８＝□□８８
由第二區的除式來判斷：（□８６╳□＝□□８）
∵□８６╳３＝□５８　可能有
　１８６╳３＝５５８　２８６╳３＝８５８　兩種
由第三區的除式來判斷：（□８□╳８＝□８□□）
∵１８６╳８＝１４８８　２８６╳８＝２２８８
∴都不合　這種情形無解。

(３)□４８╳３＝□□４４
由第二區的除式來判斷：（□４８╳□＝□□４）
∵　□４８╳３＝□□４４≠□□４
∴不合　這種情形無解。

所以這個８Ａ謎題只有１種答案。