交淺言深 ... I, U 各自展延「冪級數」了 - m ^ ^ m 計算紙「圭立及～尸非子」寫字簿

字體：小中大

交淺言深 ... I, U 各自展延「冪級數」了

2009/03/11 17:19:04瀏覽985｜回應0｜推薦0

ps~ sorry 原來俺看到的 "Lisbon story" (Wim Wenders, 1995)『里斯本的故事』( 最動人的一幕 "Guitarra" ) MV 被移除了 ~

重新找另外一人貢獻的：http://www.youtube.com/watch?v=7_bHg4QJ_Go 最動人的一幕 "Guitarra" ~

Φ Ψ

日子真好打混, 這一刻「數學」知識科學傳教, 課程竟然在看 youTube....

Ω Θ

http://blog.udn.com/lianfuplay/2523274?f_ORDER_BY=DESC&pno=41&#reply_list

udn 第 2 蛋 p.42 ~2009/01/31 20:39 ( 修正：該網址也異動過了 )

交淺言深 ~ 模擬「煮」編自 cook 自 eat 的 1 顆擺爛白煮 egg...

一言難盡她說『里斯
本的故事』看過七遍酷嗜
詩短情長寫明信片擺飾
集合論中與他聯集差集似
有若無的交集空集合又勢
如破竹各自展延冪級數心不死
一再重播潛意識中鳥不拉屎
頭重腳輕自己也不知是不是
小提琴配一把量子鑰匙
獸醫飼主即彼此懷釋

PS~

wiki ( 維基百科，自由的百科全書 )

Sigma-sign looks pretty..... The sum 1 + 2 + 3 + 4 + 5 + . . . + 10 + 11 + 12
can be written very concisely ( 簡明地 ) using the capital Greek letter as：

k=12
Σ k
k=1

...............

..............

常見的簡單有窮數列的級數包括等差數列和等比數列的級數。對於有窮數列的級數一般通過初等代數的方法就可以求得。

如果序列是無窮序列，其和則稱為無窮級數。無窮級數有發散和收斂的區別，稱為無窮級數的斂散性。判斷無窮級數的斂散性是無窮級數研究中的主要工作。無窮級數只有在收斂時才有一個和；發散的無窮級數沒有和。

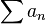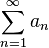對於無窮級數的研究需要更多的數學分析的方法來解決。無窮級數一般寫作 $a_1 + a_2 +a_3+ \cdots$ 、 $\sum a_n$ 或者 $\sum_{n=1}^\infty a_n$ ，級數收斂時，其和通常被表示為 $\sum_{n=1}^\infty a_n$ 。

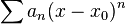形同 $\sum a_n (x- x_0)^n$ 的函數項無窮級數稱為 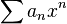$x - x 0$ 的冪級數。一般只需討論形同 $\sum a_n x^n$ 。根據阿貝爾定理，它的收斂域是一個關於零對稱的區間，即為 $( - R, R)$ （可開可閉）的形式。這個正數 R （可以是無窮大）叫做冪級數的收斂半徑。並有定理：

設冪級數 $\sum a_n x^n$ 滿足 $\lim_{n \to \infty} {a_{n+1} \over a_n} = ho$ ，則：

$ρ$ 是正實數時， $R = {1 \over ho}$ 。
$ρ = 0$ 時， $R = \infty$ 。
$ho = \infty$ 時， $R = 0$ 。

( 知識學習｜科學百科 )