@學齡前的算術教育---您是教小朋友數數還是教連數?
當我們牽著孩子的手,邁開步伐和他們一起走著,口中跟你一起數著1234.......到10,甚至到了100。這意謂著什麼呢?小朋友的記性很好,掌握語言的學習速度很快,但是我們已經帶他們進入數學教育了嗎?他們是在數數,還是在連數?數數和連數又有什麼不同呢?
數數:如字面的意思-數著數量。就是說有具體的量讓小朋友數出來,如:拿1顆蘋果給小朋友,跟小朋友說這是1顆蘋果,拿2顆蘋果,教小朋友數出1.2,這是2顆蘋果。你指著2顆蘋果時,他會告訴你這是2顆。這就是具體的數數量概念。
開始建立小朋友數數量的概念時,可以從1-10開始,不用加入任何符號,只要準備各式各樣吸引小朋友的物品(大的物品可以訓練五指的抓取,小的物件可以訓練兩指抓的精細動作),凡是可以數的,方便取得的皆可拿來當教具(見照片圖),如:石頭,彩色橡皮圈,豆子,冰棍,吸管,膠珠,棋子.......等。拿取1個具體的數量時,同時告訴小朋友這是1個,當要告訴小朋友2的數量時,只需要再多拿1個放在原本的1個的量旁邊,同時告訴小朋友1再多1,是2。以此方式具體的教授到10,非常的明確易懂,而小朋友已經開始建立連數量的概念,也同時建立每個數量前後差1的概念。
當小朋友掌握了具體的量後,再把1-10的數字(抽象符號)帶入,慢慢建立取1的量,可以拿取正確的阿拉伯數字1或是看到數字5,可以數5的量是多少。上述的就是我們如何開始建立小朋友數數的概念。
而連數的又有什麼不同呢?
當我們邁開步伐走著,小朋友跟著我們數123,其實我們是在教小朋友連數的概念,也就是這是第1步,這是第2步,這是自然數裡面的序列概念,不是數字本身所具備的量或多少,便是連數了。
所以,在算術教育中,我們要先讓小朋友具體的了解你口中所說的3(由嘴巴裡說出來的數詞),就要準備像石頭,豆子這種具體的量(數量),最後出現文字符號3這個數字,小朋友聯結了數詞/數量/數字的概念,就能掌握數的特性了。
不論是1-10,甚至是1-1000,小朋友都需要清楚地了解其數詞,數量與數字,才能輕鬆地對數進行運算。所以如果請小朋友取6顆葡萄,他卻取來了7顆,那便表示他對於量的掌握還不是很精確,我們可以請自己再數一次,讓他自己自我訂正。當然,這也代表1-10的量與數活動還要繼續進行,直到小朋友可以真正掌握才進入11-19的量與數概念。
在教授學齡前或小學學齡的算術教育時,課程安排可依年齡與小朋友的程度來進行,所教授的內容及順序是:
*1-10的量
*1-10的符號
*1-10的量與符號結合
*認識0
*奇數與偶數
*大於小於概念
*認識10的合成與分解
*11-19的量
*11-19的符號(十位數與個位數之排列)
*11-19的量與符號結合
*11-99的量
*11-99的符號
*11-99的量與符號結合
*100的量
*100的符號
*10-20-30-40-50-60-70-80-90(100是10個10的概念)
*記憶0-100數字排列
*認識十進制-個,十,百,千概念,了解10個1形成10,10個10形成百,10個百100形成1000的概念。
*1-1000數量與符號
*加法運算
--加法不進位
--加法進位
A. 加法進位可進行十位進位百位進位個十進位個十百進位
B. 十的經驗(合為0): 個位進位結合為0十進位結合為0百進
結合為0個進位+百進位結合為0個進位+十進位+百進位
結合為0
*乘法運算
--乘法不進位
--乘法進位
*減法運算
--減法不退位
--減法退位
*除法運算
--除法不借位
--除法借位
數學教育必須及早進行,方法是在具體事物加入抽象的概念。進入學校的學齡兒童常視數學為障礙,認為它十份困難,只有徧好它的人才會學得好,那是因為老師們常將抽象的數字用抽象的方式來解釋(大人提供錯誤的方法所致)。
因此,當了解了數學教育的脈絡,就可以幫助小朋友在數學領域穩穩地紥根,在無法前進的關卡前停下來,穩住腳步再前進,好好培養數學心智,迎接前方的數學之路。
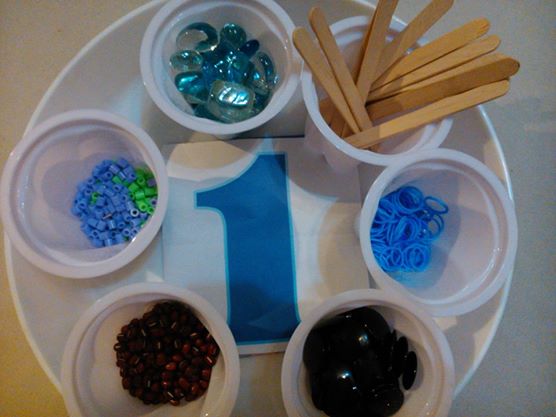


 字體:小 中 大
字體:小 中 大

 字體:小 中 大
字體:小 中 大