使用 托勒密定理 證明之。

-------------------------------------------------------------------------------------------------- 
先說一下，這是從知識家看到且搬過來，所以不是本人著作！


                                           
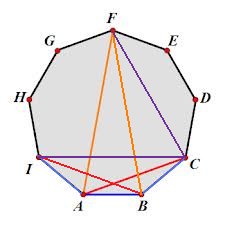
設正九邊形的邊長 AB = AI = BC = a   
最短對角線 AC = BI = b  ,  
CI = CF = c    ,  
最長對角線 FA = FB = d  。

由托勒密定理 ,
AB  * CI  +  AI  * BC  =  AC * BI  
⇒ ac + a² = b² ... (1) 

AB * CF  +  FA  * BC  =  AC * FB  
⇒ ac + da = bd ... (2)

(1) - (2) :
a² - da = b² - bd
(a - b)(a + b) = d(a - b)
a + b = d 
a  = d  - b  = 10

∴ 正九邊形的邊長 = 10    

摘自 http://tw.knowledge.yahoo.com/question/question?qid=1513081003712