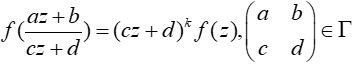字體:小 中 大
字體:小 中 大 |
|
|
|
| 2026/01/22 05:42:18瀏覽423|回應0|推薦4 | |
昨天 老友傳了一個Line給我 是關於Christopher R. Havens(1974~)從數學得到救贖與連分數的故事。 Christopher Havens目前服刑中,但遠距擔任UCLA的研究助理,專攻密碼學與連分數相關理論。 [如果您想連繫他]
陶喆軒是UCLA的教授,看看他如何看待ChatGPT錯誤的答案,以及[AI時代下的數學變革][AI在數學研究中的突破]。 要理解這篇發表在[Research in Number Theoty]論文[關於由某些非同餘算術群及超幾何級數所衍生的模形式之分類]的預備知識:
對我而言連分數略有所知,模形式則一直在虛無飄渺中。 我知道程之寧博士是弦論專家,她發現了模函數與有限對稱群間的深層關聯, 提出了著名的「伴影月光猜想」(Umbral Moonshine),揭示了這些數學結構間的精妙聯繫,對弦論、模形式與對稱性研究貢獻良多。
於是,我先請DeepSeek幫我介紹何謂模形式。 我就得到的初步訊息是: 模形式就是在複數上半平面上定義的、具有極高度對稱性(模變換下不變)且性質極好的複函數。 模變換群是SL(2,Z),建立在Poincare上半平面,但是專注於複結構(全純函數) 。
剛好我最近整理的Poincare上半平面是黎曼幾何的雙曲度量,其李代數是SL(2,R) 於是我問:我看到了Mobius transformation,這與模形式有關嗎? 以下是DeepSeek的回答: 作為幾何空間的Poincare上半平面:
幾何性質 …省略 等距變換群:保持這個度量的所有定向等距變換(全純映射)構成的群,正好是PSL(2,R)。 其作用是Mobius變換
作為模形式定義域的複上半平面: 模形式f(z)定義在同一個H上,但是我們強調它的複結構(全純函數)。 對稱性要求: 模形式要求對某個SL(2,Z)的離散子群 (稱為模群或其同餘子群)作用下
這裡SL(2,Z)是SL(2,R)的離散子群。
DeepSeek還說了一些細節,最後總結: 我們把Poincare上半平面想像成一個無限大的雙曲海洋。 SL(2,R)是這個海洋的所有連續對稱(旋轉、平移、縮放)。 SL(2,Z)是其中一個離散的「晶體對稱」子群,就像在海面上铺一张無限大的等邊三角形镶嵌(雙曲三角形镶嵌)。 模形式就是這片海洋上的一種波…
模形式與弦理論為何有關聯?最後我這樣問 DeepSeek說了: 無論是弦理論還是模形式(Modular forms),它們的核心都在於對稱性。 這種對稱性不是簡單的鏡像對稱,而是一種極其豐富、高維的「自我相似」結構。 弦理論認為,基本粒子不是「點」,而是振動著的一維弦。 這些弦在時空中運動,其世界面是一個二維的曲面。 世界面: 弦在時空中掃出的軌跡是一個二維的曲面(像一根運動的繩子掃出一個管面)。 這個曲面的幾何形狀至關重要。對於閉弦(一個圈),其世界面可以是一個環面(像甜甜圈表面)。 而這個環面的複雜結構,可以用一個複數參數 來描述,它位於複上半平面。 … 想像一個偉大的建築師(弦理論),他設計宇宙的藍圖時,規定所有基本模塊必須能無縫拼接,旋轉、鏡像後依然完美契合。 這是一個極其苛刻的要求。 結果數學家(數論與幾何)恰好早就發現了一種「魔法瓷磚」(模形式),它們天生就具有這種無論如何變換都能自我匹配的神奇屬性。 於是,建築師別無選擇,只能使用這些魔法瓷磚來建造他的宇宙。 而這些瓷磚的特殊形狀(模形式的性質),反過來決定了建築的維度(10維)和內部結構(粒子譜)。 所以,這種關係並非偶然的玄學,而是物理自洽性這一鐵律與數學內在對稱性結構之間深刻的、必然的對話。 它告訴我們,在最基礎的層面上,宇宙的構造法則可能本質上是數學的、是對稱的。這正是弦理論最吸引人也最令人驚奇的地方。 這一切 是意外 還是意料之中 您說呢 |
|
| ( 創作|另類創作 ) |



 § Modular Forms
§ Modular Forms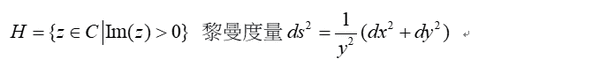
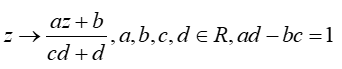 ,所以它的對稱性完全由SL(2,R)描述。
,所以它的對稱性完全由SL(2,R)描述。