字體：小 中 大 |
|
|
|
| 2008/09/21 08:09:27瀏覽9696｜回應2｜推薦10 | |
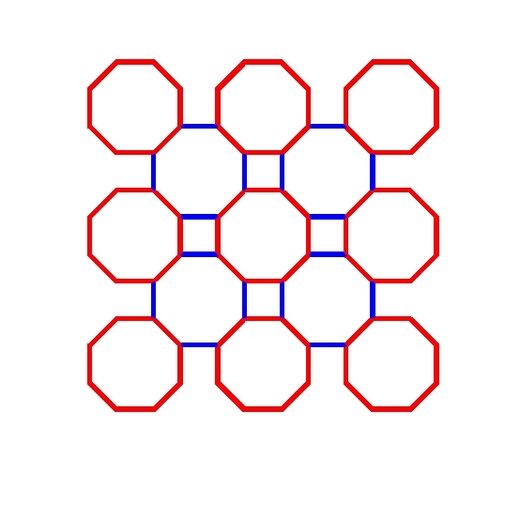
九宮八卦圖－通解（一） 半夜十二點，忽然為電話鈴聲吵醒．拿起聽筒，只聽女兒興奮地叫道：「我解出來了！我解出來了！」 我丈二金剛摸不著頭，根本不知她嚷嚷什麼，隨口問道：「解出什麼來了？」 女兒道：「還記得黃蓉說每個九宮格都可化成八卦，每個八卦的總和皆為兩百九十二嗎？」 我聞言精神大振，原來是當年黃蓉與「神算子」瑛姑間的一段公案，難得她還放在心上．今將「大漠英雄傳」中相關文字抄錄於下： 黃蓉道：「九宮每宮又可化為一個八卦，八九七十二數，以從一至七十二之數，環繞九宮成圈，每圈八字，交界之處又有四圈，一共一十三圈，每圈數字相加，均為兩百九十二。這洛書之圖變化神妙如此，諒妳也不知曉。」舉手之間，又將七十二數的九宮八卦圖在沙上畫了出來。 原來當年女兒得知有這個九宮八卦圖之後，即時常思索，想要找出這七十二個數字的排列之法．前後四、五年，終於解開此一難題． 文中所謂「九宮每宮又可化為一個八卦」，即上圖中之九個紅色正八角形；「交界之處又有四圈」，即上圖中紅藍相間的四個八角形．總共十三個八角形．一至七十二這七十二個數字排列於八角形的角上． 這七十二個數字要如何排列，才能使這十三個八角形每個總和均為兩百九十二呢？ 據女兒所言，排法總共有 36!*2^36 種（約為 2.55E52，即二點五五乘以拾的五十二次方．），排法顯然多得不得了．真的如此嗎？ 國立屏東高級中學老師羅有成帶領學生林昆餘，以研究「九宮八卦」而獲得中華民國第四十二屆中小學科學展覽會高中組數學科第三名．該研究稱排列組合共有 (9!*2!/4)^4 (6.77E+19)排法．究竟孰是孰非？或是二者皆非？ 答案如何？且聽下回分解． |
|
| ( 知識學習｜科學百科 ) |
