320x240 彩色LCD營幕的三個一組六角形之12角度旋轉的羅盤幾何圖形範例#16

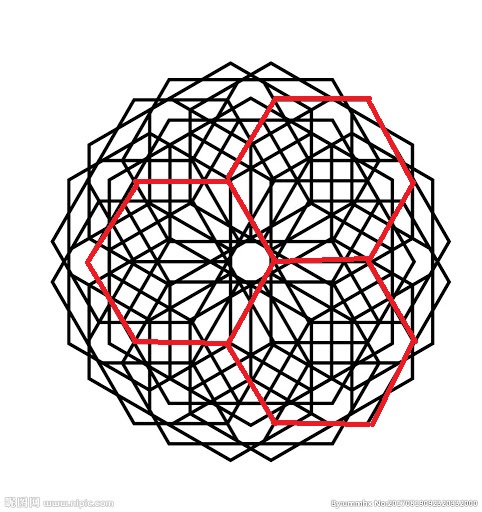
 本次的範例是根據從網路看到的一個六角形為底的羅盤幾何圖形（如下圖），興起挑戰撰寫此＂三個一組六角形之12角度旋轉的羅盤幾何圖形＂，在撰寫過程中，分成三次進化程式，先是完成三個相連的六角形，之後再進化為六角形每３０度旋轉一整圈，最後才是將其完整的完成程式，完成後的圖形，些許與原圖有所不同，不過算完成每個六角形的節點的對應位置計算方式，供各位同好參考之。

//*******  基本的六角形之三個相連
GS[0][0]=150;GS[0][1]=200;
GS[1][0]=200;GS[1][1]=200;
GS[2][0]=150+(cos(240*PI/180)*50); GS[2][1]=200+(sin(240*PI/180)*50);
GS[3][0]=200+(cos(300*PI/180)*50); GS[3][1]=200+(sin(300*PI/180)*50);
GS[4][0]=150; GS[4][1]=200+2*(sin(240*PI/180)*50);
GS[5][0]=200; GS[5][1]=200+2*(sin(240*PI/180)*50);
Line(GS[0][0],GS[0][1],GS[1][0],GS[1][1],YCOLOR[z0]);
Line(GS[0][0],GS[0][1],GS[2][0],GS[2][1],YCOLOR[2]);
Line(GS[1][0],GS[1][1],GS[3][0],GS[3][1],YCOLOR[3]);
Line(GS[2][0],GS[2][1],GS[4][0],GS[4][1],YCOLOR[4]);
Line(GS[3][0],GS[3][1],GS[5][0],GS[5][1],YCOLOR[5]);
Line(GS[4][0],GS[4][1],GS[5][0],GS[5][1],YCOLOR[6]);
GS[6][0]=GS[2][0]; GS[6][1]=200-(sin(240*PI/180)*50);
GS[7][0]=GS[3][0]; GS[7][1]=200-(sin(300*PI/180)*50);
GS[8][0]=150; GS[8][1]=200-2*(sin(240*PI/180)*50);
GS[9][0]=200; GS[9][1]=200-2*(sin(240*PI/180)*50);
Line(GS[0][0],GS[0][1],GS[6][0],GS[6][1],YCOLOR[2]);
Line(GS[1][0],GS[1][1],GS[7][0],GS[7][1],YCOLOR[3]);
Line(GS[6][0],GS[6][1],GS[8][0],GS[8][1],YCOLOR[4]);
Line(GS[7][0],GS[7][1],GS[9][0],GS[9][1],YCOLOR[5]);
Line(GS[8][0],GS[8][1],GS[9][0],GS[9][1],YCOLOR[6]);
GS[10][0]=GS[2][0]-50; GS[10][1]=GS[2][1];
GS[11][0]=GS[6][0]-50; GS[11][1]=GS[6][1];
GS[12][0]=GS[0][0]-(GS[3][0]-GS[2][0]); GS[12][1]=GS[0][1];
Line(GS[2][0],GS[2][1],GS[10][0],GS[10][1],YCOLOR[2]);
Line(GS[6][0],GS[6][1],GS[11][0],GS[11][1],YCOLOR[3]);
Line(GS[10][0],GS[10][1],GS[12][0],GS[12][1],YCOLOR[4]);
Line(GS[11][0],GS[11][1],GS[12][0],GS[12][1],YCOLOR[5]);

//****** 六角形12個角度的旋轉
r=50;
for(i=0;i<361;i+=30)
{   x0=130;
     y0=200;
     x1=x0+(cos(i*PI/180)*20);
     y1=y0+(sin(i*PI/180)*20);
  
 GS[0][0]=x1; GS[0][1]=y1;
 GS[1][0]=x1+(cos(i*PI/180)*r); GS[1][1]=y1+(sin(i*PI/180)*r);
 GS[2][0]=x1+(cos((i+240)*PI/180)*r); GS[2][1]=y1+(sin((i+240)*PI/180)*r);
 GS[3][0]=GS[1][0]+(cos((i+300)*PI/180)*r); GS[3][1]=GS[1][1]+(sin((i+300)*PI/180)*r);
 GS[4][0]=GS[2][0]+(cos((i+300)*PI/180)*r); GS[4][1]=GS[2][1]+(sin((i+300)*PI/180)*r);
 GS[5][0]=GS[3][0]+(cos((i+240)*PI/180)*r); GS[5][1]=GS[3][1]+(sin((i+240)*PI/180)*r);
 Line(GS[0][0],GS[0][1],GS[1][0],GS[1][1],YCOLOR[z1]);
 Line(GS[0][0],GS[0][1],GS[2][0],GS[2][1],YCOLOR[2]);
 Line(GS[1][0],GS[1][1],GS[3][0],GS[3][1],YCOLOR[3]);
 Line(GS[2][0],GS[2][1],GS[4][0],GS[4][1],YCOLOR[4]);
 Line(GS[3][0],GS[3][1],GS[5][0],GS[5][1],YCOLOR[5]);
 Line(GS[4][0],GS[4][1],GS[5][0],GS[5][1],YCOLOR[6]);
｝

//****  三個一組六角形之12角度旋轉的羅盤幾何圖形 - 最終程式碼
r=50;
for(i=0;i<361;i+=30)
{   x0=130;    // 中心點 x座標
 y0=180;    // 中心點 y座標
 x1=x0+(cos(i*PI/180)*20); // 以20個點半徑計算12個旋轉角度的 x1座標
 y1=y0+(sin(i*PI/180)*20); // 以20個點半徑計算12個旋轉角度的 y1座標 
 //  取得右上角的六角形之6個座標值 
 GS[0][0]=x1; GS[0][1]=y1; 
 GS[1][0]=x1+(cos(i*PI/180)*r); GS[1][1]=y1+(sin(i*PI/180)*r);
 GS[2][0]=x1+(cos((i+240)*PI/180)*r); GS[2][1]=y1+(sin((i+240)*PI/180)*r);
 GS[3][0]=GS[1][0]+(cos((i+300)*PI/180)*r); GS[3][1]=GS[1][1]+(sin((i+300)*PI/180)*r);
 GS[4][0]=GS[2][0]+(cos((i+300)*PI/180)*r); GS[4][1]=GS[2][1]+(sin((i+300)*PI/180)*r);
 GS[5][0]=GS[3][0]+(cos((i+240)*PI/180)*r); GS[5][1]=GS[3][1]+(sin((i+240)*PI/180)*r);
 Line(GS[0][0],GS[0][1],GS[1][0],GS[1][1],YCOLOR[z1]);
 Line(GS[0][0],GS[0][1],GS[2][0],GS[2][1],YCOLOR[z1]);
 Line(GS[1][0],GS[1][1],GS[3][0],GS[3][1],YCOLOR[z1]);
 Line(GS[2][0],GS[2][1],GS[4][0],GS[4][1],YCOLOR[z1]);
 Line(GS[3][0],GS[3][1],GS[5][0],GS[5][1],YCOLOR[z1]);
 Line(GS[4][0],GS[4][1],GS[5][0],GS[5][1],YCOLOR[z1]);
 // 取得右下角的六角形之另外4個座標值
 GS[6][0]=GS[0][0]+(cos((i+120)*PI/180)*r); GS[6][1]=GS[0][1]+(sin((i+120)*PI/180)*r);
 GS[7][0]=GS[1][0]+(cos((i+60)*PI/180)*r); GS[7][1]=GS[1][1]+(sin((i+60)*PI/180)*r);
 GS[8][0]=GS[6][0]+(cos((i+60)*PI/180)*r); GS[8][1]=GS[6][1]+(sin((i+60)*PI/180)*r);
 GS[9][0]=GS[7][0]+(cos((i+120)*PI/180)*r); GS[9][1]=GS[7][1]+(sin((i+120)*PI/180)*r);
 Line(GS[0][0],GS[0][1],GS[6][0],GS[6][1],YCOLOR[z1]);
 Line(GS[1][0],GS[1][1],GS[7][0],GS[7][1],YCOLOR[z1]);
 Line(GS[6][0],GS[6][1],GS[8][0],GS[8][1],YCOLOR[z1]);
 Line(GS[7][0],GS[7][1],GS[9][0],GS[9][1],YCOLOR[z1]);
 Line(GS[8][0],GS[8][1],GS[9][0],GS[9][1],YCOLOR[z1]);
 // 取得左邊的六角形之另外3個座標值
 GS[10][0]=GS[2][0]+(cos((i+180)*PI/180)*r); GS[10][1]=GS[2][1]+(sin((i+180)*PI/180)*r);
 GS[11][0]=GS[6][0]+(cos((i+180)*PI/180)*r); GS[11][1]=GS[6][1]+(sin((i+180)*PI/180)*r);
 GS[12][0]=GS[11][0]+(cos((i+240)*PI/180)*r); GS[12][1]=GS[11][1]+(sin((i+240)*PI/180)*r);
 Line(GS[2][0],GS[2][1],GS[10][0],GS[10][1],YCOLOR[z1]);
 Line(GS[6][0],GS[6][1],GS[11][0],GS[11][1],YCOLOR[z1]);
 Line(GS[10][0],GS[10][1],GS[12][0],GS[12][1],YCOLOR[z1]);
 Line(GS[11][0],GS[11][1],GS[12][0],GS[12][1],YCOLOR[z1]);
// z1++;if(z1>8) z1=1;
//  程式終點