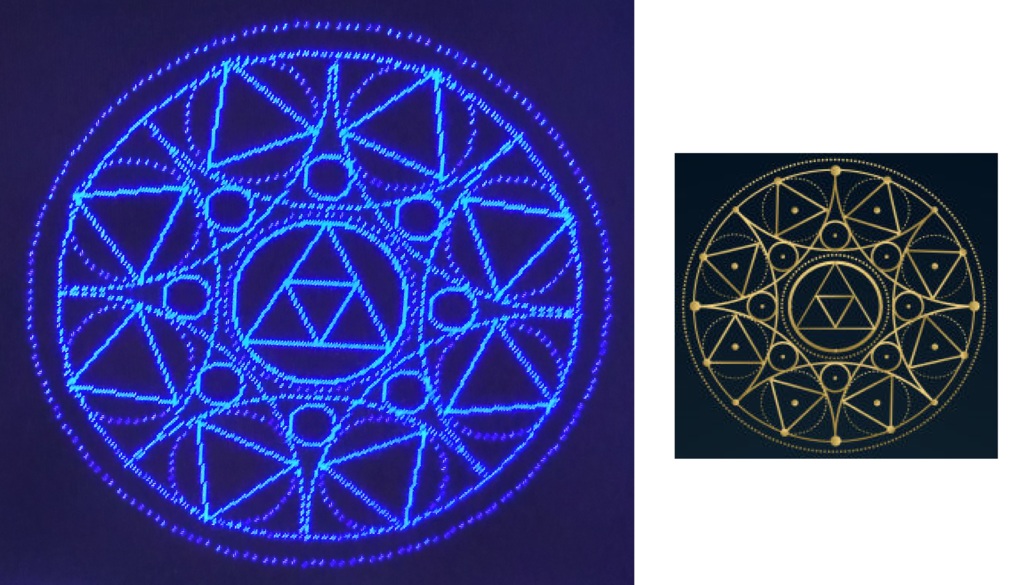
複雜幾何圖形的範例程式 - 本次的複雜幾何圖形源在挑戰繪製來先網路所看到4之圖案，加以複製而成，因為原圖之解析度甚高，在本程式所使用之LCD螢幕只有320x240點陣之下，只能大致上將基本圖形繪出，有些小形圓點就省略之，另外是程式中，有些半徑數值是以實際繪圖下調整出來的數值，未就相互的關係數學式加以計算出公式，請同好見諒，也許這也是您們可以挑戰自已的功課，試試看吧！

for(i=0;i<361;i++)
{ x0=120+(cos(i*PI/180)*30);
 y0=200+(sin(i*PI/180)*30); 
 Put_pixel(x0,y0,YCOLOR[z1]);
}
for(i=0;i<361;i++)
{ x0=120+(cos(i*PI/180)*33);
 y0=200+(sin(i*PI/180)*33); 
 if((i%5)==0) Put_pixel(x0,y0,YCOLOR[z1]);
}
for(i=0;i<361;i++)
{ x0=120+(cos(i*PI/180)*100);
 y0=200+(sin(i*PI/180)*100);
 if((i%2)==0) Put_pixel(x0,y0,YCOLOR[z1]);     
}
for(i=0;i<361;i++)
{ x0=120+(cos(i*PI/180)*90);
 y0=200+(sin(i*PI/180)*90);
 Put_pixel(x0,y0,YCOLOR[z1]);     
}
for(i=0;i<16;i++)
{ GS[i][0]=120+(cos((i*22.5)*PI/180)*70);
 GS[i][1]=200+(sin((i*22.5)*PI/180)*70);
 GS[i+16][0]=120+(cos((i*22.5)*PI/180)*46);
 GS[i+16][1]=200+(sin((i*22.5)*PI/180)*46);
}
for(j=0;j<16;j+=2)
{ for(i=0;i<361;i+=8)
 { x0=GS[j+16][0]+(cos(i*PI/180)*8);
  y0=GS[j+16][1]+(sin(i*PI/180)*8);
  Put_pixel(x0,y0,YCOLOR[z1]); 
 }
}
for(j=1;j<16;j+=2)
{ for(i=0;i<361;i+=8)
 { x0=GS[j][0]+(cos(i*PI/180)*22);
  y0=GS[j][1]+(sin(i*PI/180)*22);
  Put_pixel(x0,y0,YCOLOR[z1]); 
 }
 x1=GS[j][0]+(cos(j*22.5*PI/180)*22);
 y1=GS[j][1]+(sin(j*22.5*PI/180)*22);
 x2=GS[j][0]+(cos(((j*22.50)+120)*PI/180)*22);
 y2=GS[j][1]+(sin(((j*22.50)+120)*PI/180)*22);
 x3=GS[j][0]+(cos(((j*22.50)+240)*PI/180)*22);
 y3=GS[j][1]+(sin(((j*22.50)+240)*PI/180)*22);
 Line(x1,y1,x2,y2,YCOLOR[z1]);
 Line(x2,y2,x3,y3,YCOLOR[z1]); 
 Line(x3,y3,x1,y1,YCOLOR[z1]);
}
x1=120+(cos(30*PI/180)*30);
y1=200+(sin(30*PI/180)*30);
x2=120+(cos(150*PI/180)*30);
y2=200+(sin(150*PI/180)*30);
x3=120+(cos(270*PI/180)*30);
y3=200+(sin(270*PI/180)*30);
Line(x1,y1,x2,y2,YCOLOR[z1]);
Line(x2,y2,x3,y3,YCOLOR[z1]); 
Line(x3,y3,x1,y1,YCOLOR[z1]);
x1=120+(cos(90*PI/180)*15);
y1=200+(sin(90*PI/180)*15);
x2=120+(cos(210*PI/180)*15);
y2=200+(sin(210*PI/180)*15);
x3=120+(cos(330*PI/180)*15);
y3=200+(sin(330*PI/180)*15);
Line(x1,y1,x2,y2,YCOLOR[z1]);
Line(x2,y2,x3,y3,YCOLOR[z1]); 
Line(x3,y3,x1,y1,YCOLOR[z1]);
for(i=134;i<230;i++)
{ x1=240+(cos(i*PI/180)*85);
 y1=200+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=221;i<318;i++)
{ x1=120+(cos(i*PI/180)*85);
 y1=320+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=312;i<407;i++)
{ x1=0+(cos(i*PI/180)*85);
 y1=200+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=43;i<135;i++)
{ x1=120+(cos(i*PI/180)*85);
 y1=80+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=177;i<273;i++)
{ x0=120+(cos(45*PI/180)*90);
 y0=200+(sin(45*PI/180)*90);
 x1=x0+22+(cos(i*PI/180)*85);
 y1=y0+22+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=268;i<363;i++)
{ x0=120-(cos(45*PI/180)*90);
 y0=200+(sin(45*PI/180)*90);
 x1=x0-22+(cos(i*PI/180)*85);
 y1=y0+22+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=0;i<92;i++)
{ x0=120-(cos(45*PI/180)*90);
 y0=200-(sin(45*PI/180)*90);
 x1=x0-22+(cos(i*PI/180)*85);
 y1=y0-22+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}
for(i=88;i<182;i++)
{ x0=120+(cos(45*PI/180)*90);
 y0=200-(sin(45*PI/180)*90);
 x1=x0+22+(cos(i*PI/180)*85);
 y1=y0-22+(sin(i*PI/180)*85);
 Put_pixel(x1,y1,YCOLOR[z1]);
}