字體:小 中 大
字體:小 中 大 |
|
|
|
| 2022/06/26 06:49:25瀏覽1679|回應1|推薦35 | |
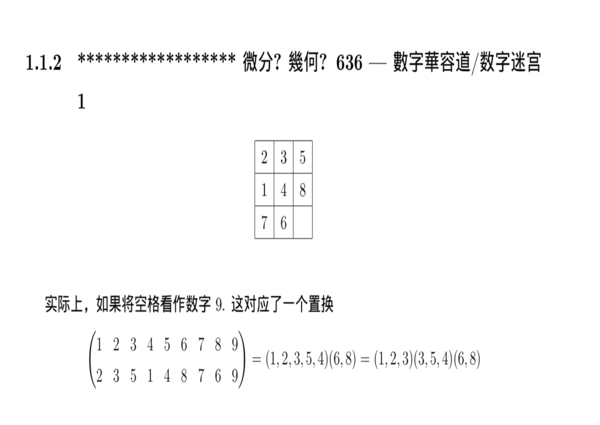
能否經由/通过一些每次改变两个元素的对换变成恒等映射?其中对换为:(i, 9)把i映成9,9映成i,其余元素不变。 有如下的疑问: (1)任给一个置换,能否写成一些对换的乘积? (2)如果置换能写成对换的乘积,那不变的东東是什么? 若游戏有解,注意到空格起始、最终位置都在右下方。所以:不管空格向上或向左移动多少次,总要向下或向右移动同样的次数,故空格总共移动偶数次。 空格9和旁边的数字做一次对换,改变一次排列的奇偶性。一共移动偶数次,如果游戏有解,最初和最终的排列的奇偶性应该相同。 (2,3,5,1,4,8,7,6,9)是奇排列,而(1,2,3,4,5,6,7,8,9)是偶排列,游戏无解。 馬拉巴栗 有氣無力 舉著盛開的花朵 |
|
| ( 不分類|不分類 ) |