關於本條目的避免深奧術語且更容易理解的版本，請見「量子力學入門」。
1927年第五次索爾維會議，此次會議主題為「電子和光子」，世界上最主要的物理學家聚集在一起討論新近表述的量子理論。
量子力學是描寫微觀物質的一個物理學分支，與相對論一起被認為是現代物理學的兩大基本支柱，許多物理學理論和科學，如原子物理學、固態物理學、核物理學和粒子物理學以及其它相關的學科，都是以量子力學為基礎。
19世紀末，古典力學和古典電動力學在描述微觀系統時的不足越來越明顯。量子力學是在20世紀初由馬克斯·普朗克、尼爾斯·波耳、沃納·海森堡、埃爾溫·薛丁格、沃爾夫岡·包立、路易·德布羅意、馬克斯·玻恩、恩里科·費米、保羅·狄拉克、阿爾伯特·愛因斯坦等一大批物理學家共同創立的。通過量子力學的發展，人們對物質的結構以及其交互作用的見解被革命化地改變，同時，許多現象也得以真正地被解釋。藉助量子力學，以往古典理論無法直接預測的現象，可以被精確地計算出來，並能在之後的實驗中得到驗證。除通過廣義相對論描寫的重力外，迄今所有其它物理基本交互作用均可以在量子力學的框架內描寫（量子場論）。
關鍵現象[編輯]
光與物質的交互作用[編輯]
黑體輻射[編輯]
19世紀末，許多物理學家對黑體輻射非常感興趣。黑體是一個理想化了的物體，它可以吸收所有照射到它上面的輻射，並將這些輻射轉化為熱輻射，這個熱輻射的光譜特徵僅與該黑體的溫度有關。但從古典物理學出發得出的有關二者間關係的公式（維因公式和瑞立－金斯公式）在輻射頻率趨向無窮大時，與實驗數據不符（被稱作「紫外災變」）。1900年10月，馬克斯·普朗克通過插值維因公式和瑞立－金斯公式，得出了一個與實驗數據完全吻合普朗克公式來描述黑體輻射。但是在詮釋這個公式時，通過將物體中的原子看作微小的量子諧振子，他不得不假設這些量子諧振子的能量不是連續的，即能量只能是離散的某些值，而不能是其他值（古典物理學的觀點恰好相反）：
這裡
是一個整數，
是一個自然常數。（後來的證明表示，正確的公式應該以
來代替，參見零點能量）。1900年，普朗克在描述他的輻射能量量子化的時候非常地小心，他僅假設被吸收和放射的輻射能是量子化的。今天這個新的自然常數被稱為普朗克常數來紀念普朗克的貢獻。其值為
Js。[1]:58-63
光電效應[編輯]
1905年，阿爾伯特·愛因斯坦擴展了普朗克的量子理論，他提出不僅僅物質與電磁輻射之間的交互作用是量子化的，而且量子化是一個基本物理特性的理論。通過這個新理論，他得以解釋光電效應。
海因里希·魯道夫·赫茲和菲利普·萊納德等人在實驗中發現，光照可以從金屬中打出電子來。同時他們可以測量這些電子的動能。不論入射光的強度，只有當光的頻率，超過一個臨限值後，才會有電子被射出。此後被打出的電子的動能，隨光的頻率線性升高，而光的強度僅決定射出的電子的數量。愛因斯坦提出了光的量子（光子這個名稱後來才出現）的理論，來解釋這個現象。光的量子的能量為
在光電效應中，這個能量被電子獲得，其中一部分被用來將金屬中的電子射出（這部分能量叫功函數，用那個
表示），另一部分被用來加速已經脫離金屬電子（這部分能量轉化為電子的動能）：
這裡
是電子的質量，
是其速度。假如光的頻率太小的話，那麼它無法使得電子獲得足夠的逸出功。這時，不論光強有多大，照射時間有多長，都不會發生光電效應。而當入射光的頻率高於極限頻率時，即使光不夠強，當它射到金屬表面時也會觀察到光電子發射。[2]:1060-1063[3]:1240-1246
原子結構[編輯]
氫原子的電子雲的機率密度：從上向下為主量子數n（1、2、3），從左向右為方位角量子數l (s、p、d)
20世紀初，拉塞福模型在當時被認為是正確的原子模型。這個模型假設帶負電荷的電子，像行星圍繞太陽運轉一樣，圍繞帶正電荷的原子核運轉。在這個過程中庫侖力與離心力必須平衡。
但是這個模型有兩個問題無法解決。首先，按照古典電磁學，這個模型不穩定。按照電磁學，電子不斷地在它的運轉過程中被加速，同時應該通過放無線電磁波喪失其能量，這樣它很快就會墜入原子核。其次，實驗結果顯示，原子的發射光譜由一系列離散的發射線組成，比如氫原子的發射光譜由一個紫外線系列（來曼系）、一個可見光系列（巴耳麥系）和其它的紅外線系列組成。按照古典理論原子的發射譜應該是連續的。
1913年，尼爾斯·波耳提出了以他名字命名的波耳模型，這個模型為原子結構和光譜線，給出了一個理論原理。波耳認為，電子只能在對應某些特定能量值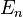
的軌道上運轉。假如一個電子，從一個能量比較高的軌道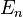（），躍到一個能量比較低的軌道（
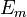）上時，它發射的光的頻率為
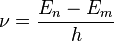
反之，電子通過吸收同樣頻率的光子，可以從低能的軌道，躍到高能的軌道上。
波耳模型可以解釋氫原子的結構。改善的波耳模型，還可以解釋只有一個電子的離子，即He+, Li2+, Be3+等。但它還不夠完善，仍然無法準確地解釋其它原子的物理現象。[1]:53-57[4]:24-29
物質繞射[編輯]
1919年，柯林頓·戴維森等人首次成功地使用電子進行了繞射實驗。路易·德布羅意由此提出粒子擁有波動性，其波長與其動量相關的理論[5]，二者關係用如下公式表示
。
簡單起見，這裡不詳細描寫戴維森等人的實驗，而是描寫電子的雙縫實驗。通過這個實驗，可以非常生動地體現出多種不同的量子力學現象。[6]
右圖顯示了這個實驗的結果：
- 打在螢幕上的電子是點狀的，這個現象與一般感受到的點狀的粒子相同。
- 電子打在螢幕上的位置，有一定的分布機率，隨時間可以看出雙縫繞射所特有的條紋圖像。假如一個光縫被關閉的話，所形成的圖像是單縫特有的波的分布機率。
在圖中的實驗裡，電子源的強度非常低（約每秒10顆電子），因此電子之間的繞射可以被排除。顯然電子同時通過了兩個縫，相互之間發生了繞射，從而導致了這個結果。對於古典物理學來說，這個解釋非常奇怪。從量子力學的角度來看，電子的分布機率和繞射結果均可以通過
這兩個通過兩個柵的、疊加在一起的狀態，簡易地演算出來。這個實驗非常明顯地顯示出了波粒二象性。
這個實驗証實了薛丁格提出的量子力學假設，即每個粒子可以被一個波函數來描寫，而這個波函數是多個不同狀態的疊加。
數學基礎[編輯]
量子力學的數學基礎是由埃爾溫·薛丁格、保羅·狄拉克、帕斯庫爾·約當和約翰·馮·諾伊曼相繼建立和嚴格化的。在這些數學框架下， 一個物理系統的量子力學描述有三個主要部分：量子態、可觀察量和動力學（即其演化），此外物理對稱性也是一個非常重要的特性。
在1926年左右，出現了兩種量子物理的理論，即維爾納·海森堡、馬克斯·玻恩和帕斯庫爾·約當的矩陣力學和薛丁格的波動力學。
1926年，薛丁格率先證明了這兩種理論的等價性。稍後，卡爾·艾卡（Carl Eckart）和沃爾夫岡·包立也給出類似證明。[1]:161-167-571927，約翰·馮·諾伊曼嚴格地證明了波動力學和矩陣力學的等價性。在這些證明過程中，尤其是馮·諾依曼的證明，量子力學被構建在無窮維可分離的希爾伯特空間之中。[7]
1930年，保羅·狄拉克出版了他的著作《量子力學原理》（Principles of Quantum Mechanics），這是整個科學史上的一個里程碑之作。狄拉克在書中引入了此後被廣泛應用的狄拉克標記和狄拉克δ函數。由此，量子力學可以表示為不依賴特定基的形式。
1936年，馮·諾依曼和賈瑞特·伯克霍夫（Garrett Birkhoff）在研究量子力學的代數化方法的基礎上發展了量子邏輯（quantum logic）。[8]量子邏輯中的格里森定理（Gleason's theorem）對量子力學測量問題有著重要的意義。
1948年左右，理察·費曼給出了量子力學的路徑積分表述。[9]
對於非相對論性的單一粒子，量子力學的數學理論基於以下公設：[10]:165-167
- 一個物理系統於時間點的狀態可以由中的一個向量來定義。這裡的希爾伯特空間指的是定義了的的。
希爾伯特空間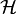
歸一化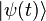
內積平方可積線性向量空間
- 每個可觀測量
可以通過狀態空間中的一個厄米算符
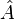來表示，可觀測量在狀態
的期望值（即測量結果的平均值）為
。進一步的，對應於可觀測量厄米算符的所有本徵態構成希爾伯特空間中正交歸一的完備函數系。任意一個態向量都可以由該算符的本徵態展開。如果系統處於算符的本徵態上，對應的可觀測量具有唯一確定的測量值，即該本徵態對應的本徵值。對於任意的態，觀測量的測量值是各本徵值的帶權平均。量子力學中的測量是不可逆的，測量後系統處於該測量值的一個特徵向量上。
- 位置算符和動量算符之間滿足正則對易關係。由此對易關係可以確定動量算符的表達式，而所有的其他算符都可以由位置算符和動量算符表出。由算符的對易式可導出不確定性原理：兩個可觀察量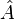和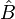
之間的不確定性為![\Delta A\Delta B \ge \left|\frac{\langle[\hat{A},\,\hat{B}]\rangle}{2i}\right|](http://upload.wikimedia.org/math/f/0/2/f0278ed6d39f98b44442f11092f5231b.png)
。
- 狀態向量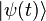的動力學演化由含時薛丁格方恆表示：
，在這裡哈密頓算符
通常對應於系統的總能量。
為了描寫無法獲得最多信息的量子狀態，物理學家創造了密度矩陣。密度矩陣包含了它所描寫的系統通過測量可以獲得的最多信息。[11]:48-55
近年來，數學家和物理學家研發出一種廣義的量子測量理論，即正定算子值測量（POVM（POVM））。[12]:179-180這種理論基本還未納入傳統的教科書中。完備正映射（completely positive maps）可以非常廣泛、而且在數學上非常優美地描寫量子系統的運算。這個新的描寫方法擴展了上面所敘述的傳統的諾伊曼方法，而且還可以描寫上述方法無法描寫的現象，比如持續性的不確定性的測量等等。[13]:89-91
量子態[編輯]
由於每一個銀原子最外層自旋1/2束縛電子的量子態只能是上旋
或下旋
，斯特恩-革拉赫實驗儀器，可以將入射的銀原子束，分裂成兩道銀原子束，每一道銀原子束代表一種量子態。
在古典力學中，一個擁有
自由度的物理系統及其隨時間的發展，可以通過對正則坐標
完全決定。在量子力學中，兩個相互共軛的可觀察量，從原則上，就無法無限精確地被測量。因此，如何相應有意義地定義一個量子物理學的系統，是一個非常基本的問題。在量子力學中，一個物理系統僅通過同時可以被測量的可觀察量來定義，這是它與古典力學最主要的區別。只有通過徹底地使用這樣的狀態定義，才能夠理論性地描寫許多量子物理現象。[4]:250ff
在量子力學中，一個物理狀態
由最多
個同時可以被測量的可觀察量定義。這些同時可以被測量的可觀察量，稱為相容可觀察量。可觀察量可以在一組特定數值取其中一個數值。可能獲得的測量值，被稱為可觀察量的本徵值。根據系統的不同，它可以是離散的，也可以是連續的。屬於這些本徵值的狀態，被稱為該可觀察量的本徵態。由於上面的定義中的可觀察量是相容的，因此它們互相之間不影響。通過使用適當的過濾，一個已知的量子物理系統，可以被預備到一個一定的狀態。以上相容可觀察量的本徵態為
這樣的狀態常被稱為「純量子態」。[14]:178-179
值得注意的是，不像古典系統那樣，這樣的量子態中，並非所有可測量的特性均被確定。對於與上述相容可觀察量不相容的物理量的本徵值，只能給出獲得一定測量值的機率，但是每個測量值肯定是其可觀察量的本徵值。這個原則性的不確定性，是從前面所提到的不確定性原理來的。它是量子力學最重要的結論，同時也是許多人反對量子力學的原因。
對於一個現有的量子物理學系統來說，一個可觀察量的本徵值，所構成的本徵態，組成一個線性的狀態空間
。從數學的角度來看這個空間是一個希爾伯特空間。這個狀態空間，表示了所有這個系統所可能擁有的狀態。因此，即使是非常簡單的量子力學系統，比如一個由量子諧振子組成的系統，它的狀態空間就已經有無限多個維了。非常重要的是多個狀態的線性組合，也是該狀態空間的一部分，即使這個線性組合，不是可觀察量的本徵態。
這個現象被稱為多個狀態的疊加。比較直觀地，這就好像一個平面內的兩個向量的和，依然是該平面內的一個向量。[4]:316ff
最簡單的一個這樣疊加的二態系統的例子是一個量子位元。
動力學演化[編輯]
量子態的動力學有不同的模型（也被稱為「繪景」）來表示。通過重新定義，算符和狀態的這些不同模型可以互相轉換，它們實際上是等價的。[14]:80-84[10]:571-574
薛丁格繪景對一個系統的動力學是這樣描述的：一個狀態由一個可導的、以時間為參量的、希爾伯特狀態空間上的函數定義。假如
是對一個時間點的狀態描述的話，那麼以下的薛丁格方程式成立：
其中，
是哈密頓算符，相當於整個系統的總能量的可觀察量，是一個自伴算符，
是虛數單位，
是約化普朗克常數。
在海森堡繪景中，狀態本身不隨時間變化，但是可觀察量的算符隨時間變化。隨時間變化的海森堡運算符由以下微分方程式定義：
![\mathrm{i}\hbar{\mathrm{d}\over \mathrm{d}t}A(t) = [A(t),H]](http://upload.wikimedia.org/math/1/9/6/196c94880b623f2f85896a661ee3ca5b.png)
通過數學演化，可以證明，假如薛丁格繪景中可觀察量不隨時間變化的話，通過薛丁格繪景和海森堡繪景獲得的的期望值是相同的。
在交互作用繪景中，狀態和算符均可隨時間變化。但是，狀態和算符的哈密頓算符不同。尤其在狀態隨時間的變化，有精確的解的情況下，這個繪景非常有用。在這個情況下，所有的數學計算，全部規限於算符的時間變化上了。因此，對於狀態的哈密頓算符被稱為「自由哈密頓算符」，對可觀察量的哈密頓算符被稱為「交互作用哈密頓算符」。動力學的發展可以由以下兩個公式來描寫：
![i\hbar{\partial\over\partial t}A(t) = [A(t),H_{\rm int}]](http://upload.wikimedia.org/math/6/f/4/6f4106b6e6517fad9235fa9698512d70.png)
海森堡繪景最類似於古典力學的模型。而從教育學的觀點來看，薛丁格繪景最容易被學生理解。互相作用繪景常被用在攝動理論中（尤其是在量子場論中）。
有些波函數形成不隨時間變化的機率分布。許多在古典力學中隨時間動態變化的過程，在量子力學中形成這樣的「定態波函數」。比如說，原子中的一顆電子，在其最低狀態下，在古典力學中，由一個圍繞原子核的圓形軌道來描寫，而在量子力學中則由一個靜態的、圍繞原子核的球狀波函數來描寫。
薛丁格方程式、海森堡方程式和交互作用繪景中的方程式均是偏微分方程式，只有在少數情況下，這些方程式才能被精確地解。雖然氦在周期表中位置僅次於氫，但是其原子的電子結構就已經無法被精確地解了。儘管如此，實際上仍有許多不同的技術來求得近似解。前面提到過的攝動理論就是一個典型的例子，它使用已知的簡單的模型系統的解來計算更複雜的模型。尤其是複雜模型中的交互作用，可以被看作是對簡單模型的「小」干擾時，這個技術特別有效。另一個技術是所謂的半古典近似，它尤其適用於量子效應比較小的系統中。
另一個計算量子力學系統的方法是理察·費曼的路徑積分表述。在這個技術中，一個量子力學系統的狀態值，等於這個系統從一個狀態過渡到另一個狀態的所有可能的路徑的可能性的和。[9]
在這裡以一個自由粒子為例。一個自由粒子的量子態，可以被一個在空間任意分布的波函數來表示。位置和動量是該粒子的可觀察量。位置的本徵態之一，是一個在特定的位置
，擁有一個巨大的值，而在所有其它位置的值為0的波函數。在這個情況下，進行一次位置測量的話，可以確定100%的可能性，該粒子位於。與此同時，其動量的本徵態是一個平面波。事實上，該平面波的波長為
，在這裡是普朗克常數，而
是該本徵態的動量。
一般來說，一個系統不會處於其任何一個可觀察量的本徵態上，但是假如我們測量一個可觀察量的話，其波函數就會立刻處於該可觀察量的本徵態上。這個過程被稱為波函數塌縮。[15]:2-5假如，我們知道測量前的波函數是怎樣的話，我們可以計算出它塌縮到不同本徵態的機率。比如一般來說，上述自由粒子的波函數是一個波包，這個波函數分布於一個平均位置
周圍。它既不是位置，也不是動量的本徵態。但假如我們測量這個粒子的位置的話，我們無法精確地預言測量結果，我們只能給出測量結果的可能性。可能我們測量到它位於附近，因為這裡的可能性最高。測量後該粒子的波函數倒塌到了一個位於測量結果的位置本徵態。
使用薛丁格方程式，來計算上述自由粒子，獲得的結果，可以看出該波包的中心，以恆定的速度在空間運動，就像在古典力學中，一個不受力的粒子一樣。但是隨著時間的發展，這個波包會越來越彌散，這說明其位置測量會越來越不精確。這也說明，隨著時間的發展，本來非常明確的位置本徵態會不斷彌散，而這個彌散的波包就已經不再是位置的本徵態了。
物理意義[編輯]
測量過程[編輯]
量子力學與古典力學的一個主要區別，在於測量過程在理論中的地位。在古典力學中，一個物理系統的位置和動量，可以同時被無限精確地確定和預言。至少在理論上，測量對這個系統本身，並沒有任何影響，並可以無限精確地進行。在量子力學中則不然，測量過程本身會對系統造成影響。[16]
要描寫一個可觀察量的測量，需要將一個系統的狀態，線性分解為該可觀察量的一組本徵態的線性組合。測量過程可以看作是在這些本徵態上的一個投影，測量結果是對應於被投影的本徵態的本徵值。假如，對這個系統的無限多個拷貝，每一個拷貝都進行一次測量的話，我們可以獲得所有可能的測量值的機率分布，每個值的機率等於對應的本徵態的係數的絕對值平方。[15]:36-37, 96-100
由此可見，對於兩個不同的物理量和
的測量順序，可能直接影響其測量結果。事實上，不相容可觀察量就是這樣的，即![[A,\,B]\neq 0](http://upload.wikimedia.org/math/9/d/8/9d85daf42020a68df39cfaabe760ded0.png)
。
不確定性原理[編輯]
最著名的不相容可觀察量，是一個粒子的位置和動量。它們的不確定性
和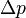
的乘積，大於或等於約化普朗克常數的一半：[15]:110-114
這個公式被稱為不確定性原理。它是由海森堡首先提出的。不確定的原因是位置和動量的測量順序，會直接影響到其測量值。海森堡由此得出結論，認為不確定性是由於測量過程的限制導致的。
通過將一個狀態分解為可觀察量本徵態
的線性組合，可以得到狀態在每一個本徵態的機率幅
。這機率幅的絕對值平方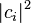
就是測量到該本徵值
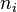的機率，這也是該系統處於本徵態的機率。可以通過將投影到各本徵態上計算出來：
因此，對於一個系綜的完全相同系統的某一可觀察量，進行同樣地測量，獲得的結果一般是不同的；除非，該系統已經處於該可觀察量的本徵態上了。通過對系綜內，每一個同一狀態的系統，進行同樣的測量，可以獲得測量值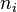的統計分布。所有實驗，都面臨著這個測量值與量子力學的統計計算的問題。[15]:160-109
全同粒子和包立原理[編輯]
由於從原則上，無法徹底確定一個量子物理系統的狀態，因此在量子力學中內在特性（比如質量、電荷等）完全相同的粒子之間的區分，失去了其意義。在古典力學中，每個粒子的位置和動量，全部是完全可知的，它們的軌跡可以被預言。通過一個測量，可以確定每一個粒子。在量子力學中，每個粒子的位置和動量是由波函數表達，因此，當幾個粒子的波函數互相重疊時，給每個粒子「掛上一個標籤」的做法失去了其意義。[15]:201ff
這個全同粒子的不可區分性，對狀態的對稱性，以及多粒子系統的統計力學，有深遠的影響。比如說，一個由全同粒子組成的多粒子系統的狀態，在交換兩個粒子「1」和粒子「2」時，我們可以證明，不是對稱的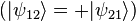
，就是反對稱的
。對稱狀態的粒子被稱為玻色子，反對稱狀態的粒子被稱為費米子。此外自旋的對換也形成對稱：自旋為半數的粒子（如電子、質子和中子）是反對稱的，因此是費米子；自旋為整數的粒子（如光子）是對稱的，因此是玻色子。
費米子的反對稱性的一個結果是包立不相容原理，即兩個費米子無法佔據同一狀態。這個原理擁有極大的實用意義。它表示，在我們的由原子組成的物質世界裡，電子無法同時佔據同一狀態，因此在最低狀態被佔據後，下一個電子必須佔據次低的狀態，直到所有的狀態均被滿足為止。這個現象決定了物質的物理和化學特性。
費米子與玻色子的狀態的熱分布也相差很大：玻色子遵循玻色-愛因斯坦統計，而費米子則遵循費米-狄拉克統計。
量子糾纏[編輯]
假設一個零自旋中性π介子衰變成一個電子與一個正電子，這兩個衰變產物各自朝著相反方向移動，雖然彼此之間相隔一段距離，它們仍舊會發生量子糾纏現象。
假設兩個粒子在經過短暫時間彼此耦合之後，單獨攪擾其中任意一個粒子，儘管兩個粒子之間可能相隔很長一段距離，還是會不可避免地影響到另外一個粒子的性質，這種關聯現象稱為量子糾纏。往往由多個粒子組成的量子系統，其狀態無法被分離為其組成的單個粒子的狀態，在這種情況下，單個粒子的狀態被稱為是糾纏的。糾纏的粒子有驚人的特性，這些特性違背一般的直覺。比如說，對一個粒子的測量，可以導致整個系統的波包立刻塌縮，因此也影響到另一個、遙遠的、與被測量的粒子糾纏的粒子。這個現象並不違背狹義相對論，因為在量子力學的層面上，在測量粒子前，你不能定義它們，實際上它們仍是一個整體。不過在測量它們之後，它們就會脫離量子糾纏的狀態。[12]:120ff
量子去相干[編輯]
作為一個基本理論，量子力學原則上，應該適用於任何大小的物理系統，也就是說不僅限於微觀系統，那麼，它應該提供一個過渡到宏觀「古典」物理的方法。量子現象的存在提出了一個問題，即怎樣從量子力學的觀點，解釋宏觀系統的古典現象。尤其無法直接看出的是，量子力學中的疊加狀態，如何應用到宏觀世界上來。1954年，愛因斯坦在給馬克斯·波恩的信中，就提出了怎樣從量子力學的角度，來解釋宏觀物體的定位的問題，他指出僅僅量子力學現象太「小」無法解釋這個問題。這個問題的另一個例子是由薛丁格提出的薛丁格貓的思想實驗。
直到1970年左右，人們才開始真正領會到，上述的思想實驗，實際上並不實際，因為它們忽略了不可避免的與周圍環境的交互作用。事實證明，疊加狀態非常容易受周圍環境的影響。比如說，在雙縫實驗中，電子或光子與空氣分子的碰撞或者發射輻射，就可以影響到對形成繞射非常關鍵的各個狀態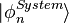
之間的相位的關係。在量子力學中這個現象，被稱為「量子去相干」。它是由系統狀態與周圍環境影響的交互作用導致的。這個交互作用可以表達為每個系統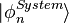狀態與環境狀態
的糾纏。其結果是只有在考慮整個系統時（即實驗系統、環境系統的總和）疊加才有效，而假如孤立地只考慮實驗系統的系統狀態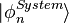的話，那麼就只剩下這個系統的「古典」分布了[17]。
| 量子去相干時間（秒）[17] |
|---|
| 自由電子 | 10微米的塵埃 | 保齡球 |
|---|
| 300K，標準氣壓 |
10-12 |
10-18 |
10-26 |
| 300K，高真空 |
10 |
10-4 |
10-12 |
| 陽光（地球表面） |
109 |
10-10 |
10-18 |
| 熱輻射（300K） |
107 |
10-12 |
10-20 |
| 宇宙微波輻射（2.73K） |
109 |
10-7 |
10-18 |
右表列出了不同物體和環境裡，量子去相干的速度。顯然即使在非常弱的環境影響下，一個宏觀物體也已經在極短的時間裡去相干了。
在上面的這個敘述中，有一個內在的假設，即去相干後的系統，自然地是我們所熟悉的古典系統。但是，這個假設並不是那麼理所當然。比如說，去相干後的宏觀系統，一般是我們所熟悉的位置狀態明確的狀態，而微觀系統則往往去相干為位置狀態不明確的狀態（比如能量特徵狀態），這是為什麼呢？這個問題的答案也來自周圍環境對系統的影響。事實上，只有不被去相干過程直接摧毀的狀態，才提供一個堅固的、去相干後的可觀察量[17][18]。
量子去相干是今天量子力學解釋宏觀量子系統的古典性質的主要方式[18]。
對於量子計算機來說，量子去相干也有實際意義。在一台量子計算機中，需要多個量子狀態儘可能地長時間保持疊加。去相干時間短是一個非常大的技術問題。
在許多現代技術裝備中，量子物理學的效應起了重要的作用。從雷射、電子顯微鏡、原子鐘到核磁共振的醫學圖像顯示裝置，都主要依靠了量子力學的原理和效應。對半導體的研究導致了二極體和三極體的發明，最後為現代的電子工業鋪平了道路。人在核武器的發明過程中，量子力學的概念也起了一個關鍵的作用。
在上述這些發明創造中，量子力學的概念和數學描述，往往很少起到直接作用，而是通過固態物理學、化學、材料科學或者原子核物理學的概念和規則，起了間接的作用。但是，在所有這些學科中，量子力學均是其基礎，這些學科的基本理論，全部是建立在量子力學之上的。
以下僅能列舉出一些最顯著的量子力學的應用，而且，這些列出的例子，肯定也非常不完全。實際上，在現代的技術中，量子力學無處不在。
原子物理和化學[編輯]
任何物質的化學特性，均是由其原子和分子的電子結構所決定的。通過解析包括了所有相關的原子核和電子的多粒子薛丁格方程式，可以計算出該原子或分子的電子結構。在實踐中，人們認識到，要計算這樣的方程式實在太複雜，而且在許多情況下，只要使用簡化的模型和規則，就足以確定物質的化學特性了。在建立這樣的簡化的模型中，量子力學起了一個非常重要的作用。
一個在化學中非常常用的模型是原子軌道。在這個模型中，分子的電子的多粒子狀態，通過將每個原子的電子單粒子狀態加到一起形成。這個模型包含著許多不同的近似（比如忽略電子之間的排斥力、電子運動與原子核運動脫離等等），但是它可以近似地、準確地描寫原子的能級。除比較簡單的計算過程外，這個模型還可以直覺地給出電子排布以及軌道的圖像描述。[15]:210-218
通過原子軌道，人們可以使用非常簡單的原則（洪德定則）來區分電子排布。化學穩定性的規則（八隅律、幻數）也很容易從這個量子力學模型中推導出來。[19][20]:931-932
通過將數個原子軌道加在一起，可以將這個模型擴展為分子軌道。由於分子一般不是球對稱的，因此這個計算要比原子軌道要複雜得多。理論化學中的分支，量子化學和計算化學，則專門使用近似的薛丁格方程式，來計算複雜的分子的結構及其化學特性的學科。[20]:235ff
原子核物理學[編輯]
是研究原子核性質的物理學分支。它主要有三大領域：研究各類次原子粒子與它們之間的關係、分類與分析原子核的結構、帶動相應的核子技術進展。[2]:1165ff
重要主題[編輯]
固態物理學[編輯]
為什麼金剛石硬、脆和透明，而同樣由碳組成的石墨卻軟而不透明？為什麼金屬導熱、導電，有金屬光澤？發光二極體、二極體和三極體的工作原理是什麼？鐵為什麼有鐵磁性？超導的原理是什麼？
以上這些例子，可以使人想像出固體物理有多麼多樣性。事實上，凝聚態物理學是物理學中最大的分支，而所有凝聚態物理學中的現象，從微觀角度上，都只有通過量子力學，才能正確地被解釋。使用古典物理，頂多只能從表面上和現象上，提出一部分的解釋。[21]
以下列出了一些特別顯著的量子現象：
量子信息學[編輯]
目前研究的焦點在於一個可靠的、處理量子狀態的方法。由於量子狀態可以疊加的特性，理論而言，量子計算機可以高度並行計算。量子系統還擁有一種特性，即對於量子數據的測量會改變數據，這種特性可以用來偵測出任何竊聽動作。倚賴這理論，量子密碼學能夠保證通信安全性，使得通信雙方能夠產生並分享一個隨機的，安全的密鑰，來加密和解密信息。另外，應用量子纏結特性與經典通訊理論，量子隱形傳態能夠將量子訊息（例如，原子或光子的量子態）從某個位置傳送至另一個位置的科技。[22]
與其它物理理論的關係[編輯]
與古典物理的界限[編輯]
1923年，尼爾斯·波耳提出了對應原理，認為量子數（尤其是粒子數）高到一定的極限後的量子系統，可以很精確地被古典理論描述。這個原理的背景是，事實上，許多宏觀系統，可以非常精確地被古典理論（如古典力學和電磁學）來描寫。因此一般認為在非常「大」的系統中，量子力學的特性，會逐漸與古典物理的特性相近似，兩者並不相抵觸。[4]:27
因此，對應原理是建立一個有效的量子力學模型的重要輔助工具。量子力學的數學基礎是非常廣泛的，它僅要求狀態空間是希爾伯特空間，其可觀察量是線性的算符。但是，它並沒有規定在實際情況下，應該選擇哪一種希爾伯特空間、哪些算符。因此，在實際情況下，必須選擇相應的希爾伯特空間和算符來描寫一個特定的量子系統。而對應原理則是做出這個選擇的一個重要輔助工具。這個原理要求量子力學所做出的預言，在越來越大的系統中，逐漸近似古典理論的預言。這個大系統的極限，被稱為「古典極限」或者「對應極限」。因此可以使用啟發法的手段，來建立一個量子力學的模型，而這個模型的極限，就是相應的古典物理學的模型。[23]:3ff
與相對論的結合[編輯]
原本量子力學的表述所針對的模型，其對應極限為非相對論性古典力學。例如，眾所皆知的量子諧振子模型使用了非相對論性表達式來表達其動能，因此，這模型是古典諧振子的量子版本。[15]:40-59
早期，將量子力學與狹義相對論聯繫到一起的試圖，涉及到使用協變方程式，例如，克萊因-戈爾登方程式或狄拉克方程式，來取代薛丁格方程式。這些方程式雖然能夠很成功地描述許多量子現象，但它們還有缺陷，尤其是它們無法描述相對論性狀態下，粒子的產生和消滅。隨著量子場論的關鍵發展，才產生了完整相對論性量子理論。量子場論不但將可觀察量（如能量或者動量）量子化了，而且將媒介交互作用的場量子化了。第一個完整的量子場論是量子電動力學，它可以完整地描寫電磁交互作用。[14]:486-514
一般在描述電磁系統時，不需要使用到完整的量子場論。比較簡單的方法，是將帶電粒子當作處於古典電磁場中的量子力學物體。這個手段從量子力學的初期，就已經被使用了。比如說，氫原子的電子狀態，可以近似地使用古典的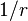
庫侖勢來計算。這就是所謂的半古典方法。但是，在電磁場中的量子起伏起一個重要作用的情況下（比如帶電粒子發射一顆光子）這個近似方法就失效了。[15]:145-160
強交互作用和弱交互作用[編輯]
專門描述強交互作用、弱交互作用的量子場論已發展成功。強交互作用的量子場論稱為量子色動力學，這個理論描述亞原子粒子，例如夸克、膠子，它們彼此之間的交互作用。弱交互作用與電磁交互作用也被統一為單獨量子場論，稱為電弱交互作用。[2]:1234-236
萬有引力[編輯]
量子重力是對重力場進行量子化描述的理論，屬於萬有理論之一。物理學者發覺，建造重力的量子模型是一件非常艱難的研究。半經典近似是一種可行方法，推導出一些很有意思的預測，例如，霍金輻射等等。可是，由於廣義相對論（至今為止，最成功的重力理論）與量子力學的一些基礎假說相互矛盾，表述出一個完整的量子重力理論遭到了嚴峻阻礙。嘗試結合廣義相對論與量子力學是熱門研究方向，為當前的物理學尚未解決的問題。當前主流嘗試理論有：超弦理論、迴圈量子重力理論等等。[24][25]
解釋和哲學觀點[編輯]
量子力學可以算作是被驗證的最嚴密的物理理論之一了。至今為止，所有的實驗數據均無法推翻量子力學。大多數物理學家認為，它「幾乎」在所有情況下，正確地描寫能量和物質的物理性質。雖然如此，量子力學中，依然存在著概念上的弱點和缺陷，除上述的萬有引力的量子理論的缺乏外，至今為止對量子力學的解釋存在著爭議。[26]
從初始，量子力學的各種反直覺論述與結果引起在哲學、詮釋方面的強烈辯論。甚至基礎論點，例如，馬克斯·玻恩關於機率輻與機率分佈的基本定則，也需要經過數十年的嚴格思考論證，才被學術界與權威物理學者接受。理察·費曼曾經說過一句銘言：「我認為我可以有把握地說，沒有人懂得量子力學！」[27]
愛因斯坦（他認為「量子力學不完備」、「上帝不擲骰子」）與尼爾斯·波耳（「上帝擲骰子」）是最早對這個問題進行爭論的。波耳維護不確定原理和互補原理。在多年的、激烈的討論中，愛因斯坦不得不接受不確定原理，而波耳則削弱了他的互補原理，這最後導致了今天的哥本哈根詮釋。二人的爭論被認為是科學史上最巔峰的學術交鋒之一。[28]
今天，大多數物理學家，接受了量子力學描述所有一個系統可知的特性，以及測量過程無法改善，不是因為我們的技術問題所導致的的見解。這個解釋的一個結果是，測量過程打擾薛丁格方程式，使得一個系統塌縮到它的本徵態。除哥本哈根詮釋外，還有人提出過一些其它解釋方式。其中比較有影響的有：
- 提出了一個不局部的，帶有隱變數的理論（（））。在這個解釋中，波函數被理解為粒子的一個引波。從結果上，這個理論預言的實驗結果，與非相對論哥本哈根詮釋的預言完全一樣，因此，使用實驗手段無法鑒別這兩個解釋。雖然這個理論的預言是決定性的，但是由於不確定原理無法推測出隱變數的精確狀態，其結果是與哥本哈根詮釋一樣，使用這來解釋實驗的結果，也是一個機率性的結果。至今為止，還不能確定這個解釋是否能夠擴展到相對論量子力學上去。和其他人也提出過類似的隱藏係數解釋。戴維·玻姆隱變數理論Hidden variable theory路易·德布羅意[29][30]
- 休·艾弗雷特三世提出的多世界詮釋認為，所有量子理論所做出的可能性的預言，全部同時實現，這些現實成為互相之間一般無關的平行宇宙。在這個詮釋中，總的波函數不塌縮，它的發展是決定性的。但是由於我們作為觀察者，無法同時在所有的平行宇宙中存在，因此，我們只觀察到在我們的宇宙中的測量值，而在其它宇宙中的平行，我們則觀察到其他宇宙中的測量值。這個詮釋不需要對測量的特殊的對待。薛丁格方程式在這個理論中所描寫的也是所有平行宇宙的總和。[31][32]
- 另一個解釋方向是將古典邏輯改成一個量子邏輯（Quantum logic）來排除解釋的困難。[33]
以下列舉了對量子力學的解釋，最重要的實驗和思想實驗：
- （EPR悖論）凸顯出局域實在論與量子力學完備性兩者之間的矛盾。假若局域實在論成立，則可以推導出量子力學的不完備性。1964年，物理學者發表，證明這個假設與量子力學的預測不相符。1982年，的初始實驗，以及後來多位物理學者專門檢驗貝爾定理而完成的一系列實驗，它們所獲得的實驗結果，證實與量子力學的預測相符合，同時證實局域實在論不成立。愛因斯坦-波多爾斯基-羅森悖論約翰·貝爾貝爾定理阿蘭·阿斯佩
- 雙縫實驗是一個非常重要的量子力學實驗，最初由托馬斯·楊作出，從這個實驗中，也可以看到量子力學的測量問題和解釋的困難性。這是最簡單而明顯地顯示波粒二象性的實驗了。
- 薛丁格貓是薛丁格於1935年提出的悖論，使得量子疊加態的現象從微觀拓展到宏觀。通過一隻處在「生存與死亡疊加態」的貓來表達對哥本哈根詮釋的懷疑。
哲學問題[編輯]
量子力學的許多解釋，涉及到一般的哲學問題，這些問題又涉及到本體論、認識論和科學哲學的基本概念和理論。以下為一些這些問題：
- ^ 反對稱性波函數為
![[\sin(x)sin(3y)-sin(3x)sin(y)]/\sqrt{2},\qquad 0\le x,y \le \pi](http://upload.wikimedia.org/math/1/8/2/18296b149f5f90b2475ec64ead94ee69.png)
。注意到在
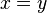附近，機率輻絕對值很微小，兩個費米子趨向於彼此互相遠離對方。
- ^ 對稱性波函數為
![-[\sin(x)sin(3y)+sin(3x)sin(y)]/\sqrt{2},\qquad 0\le x,y \le \pi](http://upload.wikimedia.org/math/f/8/7/f87cc625764a4323327b6df570b2c2ce.png)
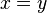。注意到在附近，機率輻絕對值較大，兩個費米子趨向於彼此互相接近對方。
參考文獻[編輯]
- ^ 1.0 1.1 1.2 Kragh, Helge. Quantum Generations: A History of Physics in the Twentieth Century Reprint. Princeton University Press. 2002. ISBN 978-0691095523.
- ^ 2.0 2.1 2.2 Halliday, David; Resnick, Robert; Walker, Jerl, Fundamental of Physics. 7th, USA: John Wiley and Sons, Inc.. 2005, ISBN 0-471-23231-9
- ^ Serway, Raymond; Jewett, John. Physics for Scientists and Engineers with Modern Physics 9th. Cengage Learning. 2013. ISBN 978-1133954057.
- ^ 4.0 4.1 4.2 4.3 French, Anthony, An Introduction to Quantum Physics, W. W. Norton, Inc.. 1978, ISBN 0-393-09106-0
- ^ Davisson, Clinton. The Discovery of Electron Waves//Nobel Lectures, Physics 1922-1941. Amsterdam: Elsevier Publishing Company. 1965 [2007-09-17].
- ^ 費曼, 理查; 雷頓, 羅伯; 山德士, 馬修. 費曼物理學講義III (1)量子行為. 台灣: 天下文化書. 2006: pp. 38–60. ISBN 986-417-672-2.
- ^ von Neumann, John. Mathematical Foundations of Quantum Mechanics 1996. Princeton Univ. Press. 1932. ISBN 0-691-02893-1.
- ^ G. Birkhoff and J. von Neumann, The Logic of Quantum Mechanics, Annals of Mathematics, Vol. 37, pp. 823–843, 1936.
- ^ 9.0 9.1 Feynman, Richard P. (Richard Phillips); Hibbs, Albert R.; Styer, Daniel F. Quantum Mechanics and Path Integrals. Mineola, N.Y.: Dover Publications. 2010. ISBN 0-486-47722-3.
- ^ 10.0 10.1 Nouredine Zettili. Quantum Mechanics: Concepts and Applications. John Wiley & Sons. 17 February 2009. ISBN 978-0-470-02678-6.
- ^ Ballentine, Leslie. Quantum Mechanics: A Modern Development 2nd, illustrated, reprint. World Scientific. 1998. ISBN 9789810241056.
- ^ 12.0 12.1 Laloe, Franck, Do We Really Understand Quantum Mechanics, Cambridge University Press. 2012, ISBN 978-1-107-02501-1
- ^ Stéphane Attal; Alain Joye; Claude-Alain Pillet. Open Quantum Systems III: Recent Developments. Springer. 26 July 2006. ISBN 978-3-540-30993-2.
- ^ 14.0 14.1 14.2 Sakurai, J. J.; Napolitano, Jim, Modern Quantum Mechanics. 2nd, Addison-Wesley. 2010, ISBN 978-0805382914
- ^ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 15.7 Griffiths, David J., Introduction to Quantum Mechanics (2nd ed.), Prentice Hall. 2004, ISBN 0-13-111892-7
- ^ Krips, Henry. Measurement in Quantum Theory. Stanford Encyclopedia of Philosophy. Aug 22, 2007.
- ^ 17.0 17.1 17.2 E. Joos et al. Decoherence and the Appearance of a Classical World in Quantum Theory. Springer. 2003. ISBN 3-540-00390-8.
- ^ 18.0 18.1 Schlosshauer, Maximilian. "Decoherence, the Measurement Problem, and Interpretations of Quantum Mechanics". Reviews of Modern Physics.
- ^ Langmuir, Irving. The Arrangement of Electrons in Atoms and Molecules. Journal of the American Chemical Society. 1919, 41 (6): 868–934. doi:10.1021/ja02227a002.
- ^ 20.0 20.1 David W. Oxtoby; H. Pat Gillis; Alan Campion. Principles of Modern Chemistry, 7th ed.. Cengage Learning. May 2011. ISBN 978-0-8400-4931-5.
- ^ Kittel, Charles, Introduction to Solid State Physics. 8th, USA: John Wiley & Sons, Inc.. 2005, ISBN 978-0-471-41526-8
- ^ Michael A. Nielsen; Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press. 9 December 2010. ISBN 978-1-139-49548-6.
- ^ J.R. Nielsen. The Correspondence Principle (1918 - 1923). Elsevier. 1 January 1976. ISBN 978-0-08-087101-1.
- ^ Smolin, Lee. Three Roads to Quantum Gravity. 129–148. 2001. ISBN 0-465-07835-4.
- ^ Kiefer, Claus. Quantum Gravity: General Introduction and Recent Developments. Annalen der Physik. 2005, 15: 129–148. arXiv:gr-qc/0508120. Bibcode:2006AnP...518..129K. doi:10.1002/andp.200510175.
- ^ 曾謹言. 量子力學教程：量子力學百年. 科學出版社. . ix-xxi. ISBN 7-03-010982-1.
- ^ The Character of Physical Law (1965) Ch. 6; also quoted in The New Quantum Universe (2003), by Tony Hey and Patrick Walters
- ^ 愛因斯坦對玻爾，物理學史上最偉大的交鋒. 新京報. 2005-10-06 [2013-09-01].
- ^ Bohm, David. A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I. Physical Review. 1952, 85: 166–179. Bibcode:1952PhRv...85..166B. doi:10.1103/PhysRev.85.166. (full text)
- ^ Bohm, David. A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables", II. Physical Review. 1952, 85: 180–193. Bibcode:1952PhRv...85..180B. doi:10.1103/PhysRev.85.180. (full text)
- ^ Hugh Everett. Theory of the Universal Wavefunction. Princeton University. 1956, 1973. 1-140.
- ^ Everett, Hugh. Relative State Formulation of Quantum Mechanics. Reviews of Modern Physics. 1957, 29: 454–462. Bibcode:1957RvMP...29..454E. doi:10.1103/RevModPhys.29.454.
- ^ D. Cohen. An Introduction to Hilbert Space and Quantum Logic. Springer-Verlag. 1989.
外部連結[編輯]
字體：小 中 大
.jpg)
