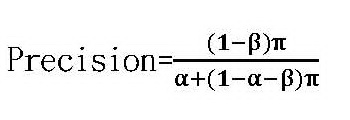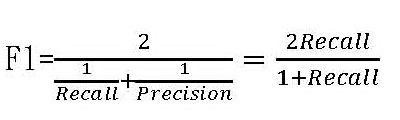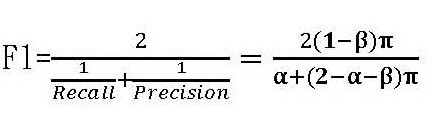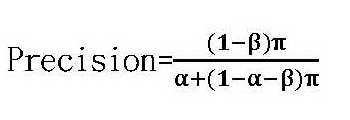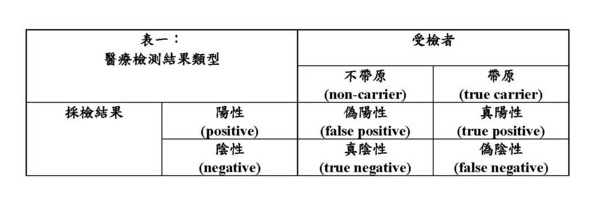
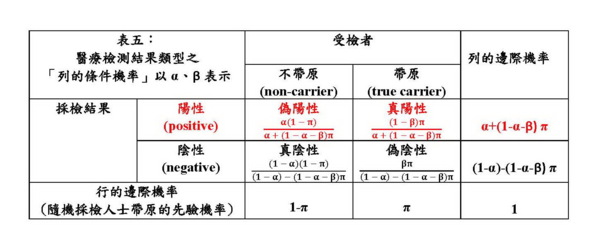
最近因為大家關心新冠病毒是否要全面篩檢的問題，媒體上常見一些醫事檢驗學的術語。其中最常聽到的是「偽陰性」，但也常讀到「特異性」與「敏感性」；這些名詞都與新冠病毒檢測的準確度有關。在瘟疫變成每個人生存威脅的時候，這些專門術語也變得跟我們的生活息息相關。本文嘗試用基本統計檢定概念來詮釋這些名詞，更進一步用數據科學中衡量搜尋、辨識工具準確度的概念來探討醫療檢測的準確度。

一、檢測準確度的相關概念

在醫檢學，「敏感性」(sensitivity)常與「特異性」(specificity)共同用來衡量檢測的準確度。這些名詞，不熟悉醫檢學的讀者可能會覺得莫測高深，但其實它們與基本統計學所教的統計檢定的基本概念是互相對應的，只是著重點有所不同。這裡先簡單地解釋它們與統計檢定概念的關係，以利讀者了解醫檢學的術語。

先說特異性。特異性是不帶原者中採檢陰性的比例，一般簡稱為「真陰性」的比例。而敏感性則是帶原者中採檢陽性的比例，也可稱為「真陽性」的比例。見表一：

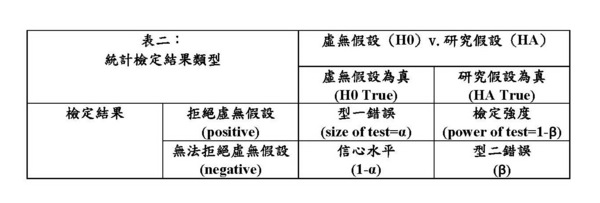
如果把上圖跟基本統計學學生所熟悉的下圖相比較，就可以看出醫檢術語與傳統統計檢定概念的對應關係。見表二：

所以當我們把「比例」視同「機率」時，特異性其實就是統計檢定的信心水平，而敏感性就是統計強度。連結到型一錯誤的機率α(即顯著水平，也稱檢定規模)、型二錯誤的機率β，可以清楚看到,

特異性=真陰性的機率=信心水平=1-α

敏感性=真陽性的機率=檢定強度=1-β

因為α、β是錯誤的機率，愈小愈好，所以特異性、敏感性都是愈高愈好。但α、β並不是互相獨立的。如果樣本數固定、所要檢定的效應（即H0跟HA的差距）也固定，通常α愈小β會愈大、α愈大β會愈小，因此特異性跟敏感性之間也有同樣的互換關係。

特異性、敏感性這兩個概念其實都還是傳統所謂「頻率學派」(frequentist)統計學的概念，它們並未涉及貝氏定理的反機率。在討論新冠病毒採檢準確度的問題時，我們更需關注的其實是反機率的問題: 「當採檢為陽性時，其為偽陽性的機率有多高?」 反過來說,「當採檢為陰性時，其為偽陰性的機率有多高?」 這些問題，也是近年來撼動頻率學派統計檢定方法的貝氏學派統計學者所指出的問題。要算這些反機率就必須用到貝氏定理。最近在機器學習、自然語言處理等領域被廣泛使用的F1便是由「真陽性」的機率與反機率混合組成的一種檢測準確度（accuracy）的度量。

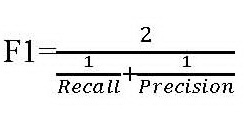
二、數據科學中辨識準確度：F1分數

F1分數有時簡稱F分數, 也稱為Sørensen-Dice係數。在數據科學裡，F1常被用來做為搜尋、辨識「相似」資料準確度的度量。它可以用來衡量搜尋引擎的準確度，也常用在自然語言處理中資料的搜尋、辨識，當然它也可以用於人臉辨識。

想像你要用文本分析的方法來研究瘟疫流行期間海峽兩岸情緒的互動。台灣這邊，你要找出一月以來所有與疫情及兩岸情緒互動有關的貼文；大陸那邊，你專注於搜尋微信上面的貼文。你使用的辨識工具是一組包括疫情及兩岸關係的關鍵詞；你希望這組關鍵詞能夠正確地指認出每一篇相關貼文。你知道你的辨識工具的準確度跟你使用的關鍵詞有關，為了要正確找出相關貼文，你希望辨識的準確度越高越好；但是不論你使用了哪些關鍵詞，你的工具的準確度不會是百分之百。有時一篇貼文明明跟你研究的主題有關，你的辨識工具卻指認不出來；有時明明跟研究主題無關的貼文，卻被認定有關。這樣的文本處理過程，其實與醫療檢測有類似之處：對同一篇貼文，用關鍵詞為工具來辨識貼文性質的結果可以有偽陽性、真陽性、真陰性、偽陰性四種類型。這基本上跟表一是一樣的。

F1包含了兩個成分：召回率（Recall）和精密性（Precision）。F1是這兩個成分的平均數，但不是算數平均數而是調和平均數：

因為召回率和精密性的值都介於0與1之間，F1的值也會介於0與1之間。如果召回率和精密性之一的值趨近於0，F1的值也會趨近於0；如果召回率和精密性的值都等於1，F1的值也會等於1。特別值得注意的是：作為調和平均數，F1的值永遠小於或等於召回率和精密性的算術平均數。這也就是說：相較於算術平均數，F1的值會更被它的成份中比較小的那個數值拉低。不論召回率和精密性之中哪個成分的值較小，在計算F1時．較小那個成分實質上有較大的權重。這是調和平均數與算數平均數不同的地方。

那麼什麼是召回率？什麼是精密性？

召回率其實就是醫檢學中的敏感性（真陽性）。之所以喚作召回率，應該就是真正具有某種性質的受檢群體有多少比例能夠被正確指認出來的意思。召回率可以用型二機率表示如下：

召回率=敏感性=真陽性的機率=Pr(採檢結果陽性|受採檢者為帶原者)=1-β

精密性則是召回率的反機率：

精密性=召回率（敏感性、真陽性）的反機率=Pr(受採檢者為帶原者|採檢結果陽性)

為什麼算準確度除了召回率還要加上召回率的反機率？這是因為反機率其實是更實際、更重要的考慮。召回率的分母是不特定的群體，而精密性（召回性的反機率）的分母是特定的。以醫療檢測來說，召回率（敏感性）的分母包括所有帶原者，但受採檢的個人並不知道自己帶不帶原，採檢的防疫人員也不知道帶原者是哪一群人，因此召回率只是一個抽象的概念。相對來說精密性（敏感性的反機率）的分母是所有採檢陽性者，不但採檢陽性的個人知道自己是陽性，防疫人員也知道採檢陽性的是哪一群人，因此它是比較具體的概念。採檢陽性的人會亟想知道自己是真正帶原還是不帶原，防疫人員更需要考量採檢陽性的人中有多少真正帶原或其實不帶原。

用貝氏定理計算反機率的詳細步驟，請參考林澤民、吳俊穎〈貝氏定理在生活中很有用，可是它到底怎麼算？〉以及本文附錄。但貝氏定理要求必須先對帶原、不帶原的先驗機率作出假設。我們假設所有受檢者中帶原者的比例為π——或者說每一隨機受檢者帶原的機率為π——而不帶原的比例為1-π。這π可以是客觀估計的頻率也可以是醫生經由對受檢者問診或疫調形成的主觀判斷。我們算出的結果是：

精密性（敏感性的反機率）可能甚小於敏感性。例如當π=0.1，α=0.05，β=0.2時，敏感性為0.8，敏感性的反機率約為0.14。這是因為採檢陽性者當中有甚多是偽陽性者的緣故。假設桃園機場每天有1000位入境旅客全部接受篩檢，其中未帶原者有990人而帶原者只有10人。雖然偽陽性（α）只有5%，990位未帶原者中也會有將近50被誤檢為陽性，而真陽性（1-β）雖然高達80%，10位帶原者中也只有8位確診陽性。這樣採檢陽性者一共58人中，帶原者的比例也只有8/58，大約14%。

從精密性的公式可以看出：當α=0，特異性100%的時候，精密性也是100%。此時F1的公式簡化為

也就是F1完全由召回率（敏感性、真陽性）來決定，召回率越高F1也越高；此時沒有反機率的問題。

三、F1在新冠狀病毒檢測的應用

要用F1來衡量醫事檢驗的準確度，只要把召回率改成敏感性（真陽性）、把精密性改成敏感性（真陽性）的反機率就可得到下列F1分數：

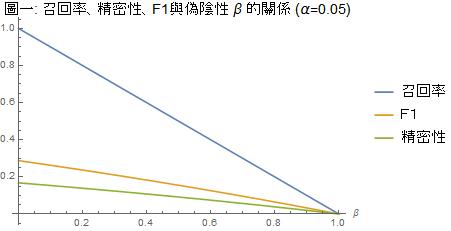
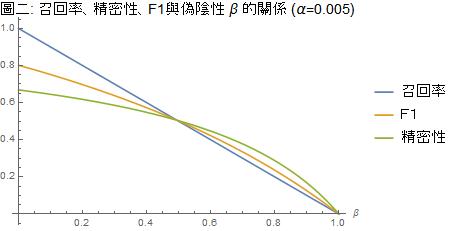
這個公式包含了三個變項：α、β、π。在醫學檢驗，α是偽陽性也是特異性的反面，β是偽陰性也是敏感性的反面。在統計分析中，α是研究者自己可以設定的，就是一般所謂的顯著水平，通常設在α=0.05。近年因為學界廣泛對p值的質疑，有不少學者主張要從嚴用α=0.005。在採檢新冠狀病毒的時候，核酸檢測的設計極大化了特異性，也就是極小化了偽陽性的機率α；快篩則因為較難以區別各種冠狀病毒而會有較大的α。圖一、二中，我們分別以α=0.05及α=0.005這兩個顯著水平為參數，在所有受檢者中帶原者的比例π=0.01的假設下，劃出召回率（敏感性、真陽性）、精密性（敏感性、真陽性的反機率）、F1對於β的函數圖形。

這兩個圖形的橫軸，β，是型二錯誤機率，也即偽陰性，它是敏感性（真陽性）1-β的反面。偽陰性是防疫專家很關心的一個指數；防疫中心指揮官陳時中之所以堅持不肯在機場對入境旅客進行普篩的主要原因就是因為篩檢的偽陰性高，他擔心旅客採檢陰性就放下心防趴趴走。若偽陰性的檢測結果太多，則病毒將在社區廣泛傳播。防疫中心似乎從不曾明確說出快篩偽陰性的機率，張上淳醫師則說他相信三採陰的核酸檢測敏感性「幾乎是百分之百」。中文網頁曾被引用的敏感性數字如「約10%~70%」、「只有50-80%」等，似乎指的都是流感的快篩而不是新冠狀病毒的快篩。其實，即使4月9日的Science Daily都還引用一篇Mayo Clinic Proceedings的論文指出醫學文獻尚未就現有核酸檢測工具的敏感性有清楚、一致的報告。如果快篩敏感性「只有50-80%」，那我們必須考慮的β數值應在20-50%之間。如果偽陰性的機率是0.2，三採陰性仍為偽陰性的機率是0.008，那麼三採陰的敏感性的確是張上淳醫師所說的「幾乎是百分之百」。

然而敏感性並不是計算準確度的唯一成分，除了敏感性，我們還要考慮敏感性的反機率。圖一、二顯示，至少在0<β<0.5的區間，精密性（敏感性的反機率）要小於召回率（敏感性），而兩者的和諧平均數F1要比算術平均數更靠近數值較低的精密性。換句話說，當我們在計算準確度時，因為把敏感性的反機率納入考慮，準確度會被拉低。

接續前面的例子，當p=0.1，α=0.05，β=0.2時，敏感性為0.8，敏感性的反機率為0.14，準確度F1只有不到0.24!

如果我們把α從嚴降低到α=0.005，則β=0.2時，敏感性仍然為0.8，敏感性的反機率為0.62，準確度F1可以提高到0.70。

如果這樣的準確度仍然不令人放心，那只好「順時中」以三採陰性才算真陰性。如此偽陰性的機率降低到β=0.008，敏感性增為0.992，敏感性的反機率為0.667，準確度F1可以提高到將近0.80。但是多重採檢也有可能出現統計檢定中所謂「多重假說檢定」（multiple hypothesis test）的問題。例如在α=0.05時，對一位實際不帶原者進行三次採檢，理論上得到至少一次偽陽性的機率是1-(1-0.05)^3=0.1426，採檢越多次這個機率越大。其實，即使偽陰性降到0、敏感性達到百分之百，敏感性的反機率仍然只有0.67，F1還是只有比0.80高一點點。

這癥結所在就不再是敏感性的問題而是特異性（1-α）的問題了，只有把偽陽性的機率α降到更小，讓特異性趨近百分之百，這樣才能解決反機率的問題，讓F1完全由召回率（敏感性、真陽性）來決定。然而即使核酸檢測能做到這樣，快篩卻不一定行。根據報載，中研院基因體研究中心所發展出來的快篩試劑可以達到95%以上的特異性。雖然如此，如圖一所示，在α=0.05的水平，敏感性的反機率其實是非常值得注意的問題。只要普檢仰賴快篩，我們便不能只以特異性及敏感性來衡量醫療檢測的準確度。

附錄: 如何計算精密性——敏感性（真陽性）的反機率？

敏感性的反機率如何計算？在〈貝氏定理在生活中很有用，可是它到底怎麼算？〉一文中我提出一個計算貝氏機率的捷徑：從「行的條件機率」為出發點，貝氏定理所要求的反機率就是「列的條件機率」。如果採取這個觀點，則不需要死背難記的公式就能計算反機率。這包括兩個步驟：

（1）把「行的條件機率」乘上「行的邊際機率」就可以得到「聯合機率」。

（2）把「聯合機率」除以「列的邊際機率」就可以得到「列的條件機率」。

這裡「行的邊際機率」就是算貝氏定理必需要先知道的「先驗機率」。至於「列的邊際機率」則把各列的聯合機率相加就可求得。

表三顯示醫事檢驗結果類型以α、β表示之「行的條件機率」。我們假設所有受檢者中帶原者的比例為π——或者說每一隨機受檢者帶原的機率為π——而不帶原的比例為1-π。這π的值通常不難估計，即使無法估計也可以假設不同的數值做為討論基礎，有更多資訊時再求改進。π與1-π是「行的邊際機率」，也就是「先驗機率」。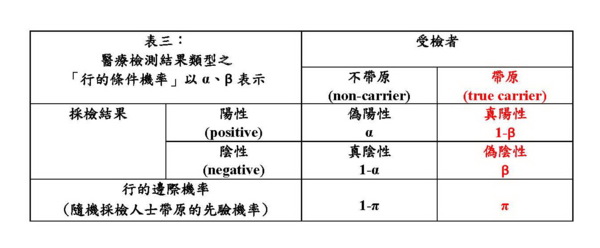

有了「行的條件機率」和「先驗機率」，我們依步驟（1）算得四種類型的「聯合機率」，如表四。再依步驟（2），我們很容易依次算得「列的邊際機率」及「列的條件機率」如表五。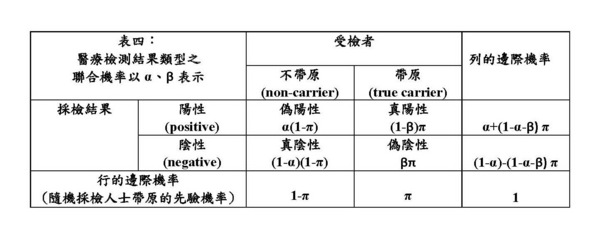

所以敏感性（真陽性）的反機率是：